Chapter 1: The Iceberg Phenomenon

Imagine an iceberg adrift in the ocean.

What fraction of this iceberg is visible above the waterline? In other words, what is the percentage representing the "tip of the iceberg"?

Assuming the density of seawater is approximately 1,024 kg/m³ and that of ice is 917 kg/m³, we can designate:

• V as the total volume of the iceberg,
• v as the volume of the iceberg submerged in seawater,
• ?_s as the density of seawater,
• ?_i as the density of ice.

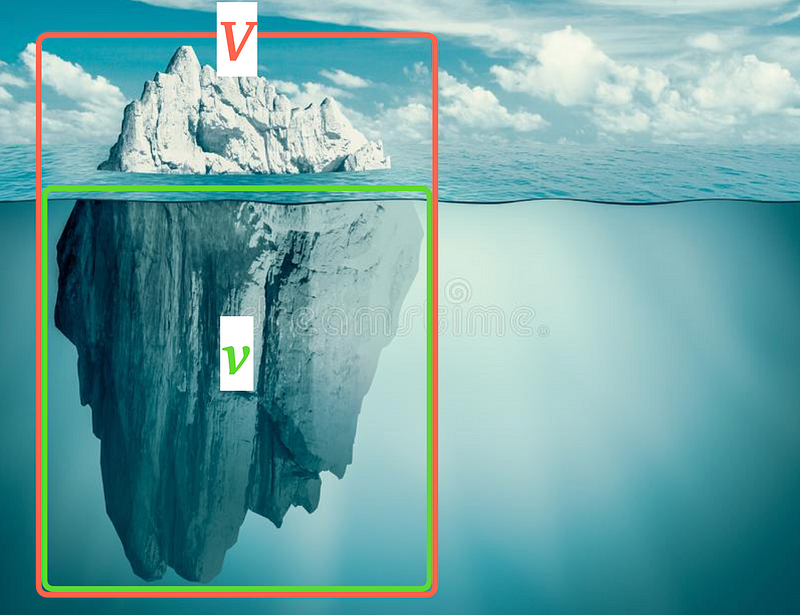
The volume above water can be expressed as (V - v), while the total volume is V. Thus, to determine the fraction of the iceberg above water, we compute (V - v)/V. Converting this ratio to a percentage yields:

To simplify, we only need to ascertain the value of v/V. Given that the iceberg is neither sinking nor rising, it remains in equilibrium, indicating that the forces acting on it are balanced.

What forces are at play here?

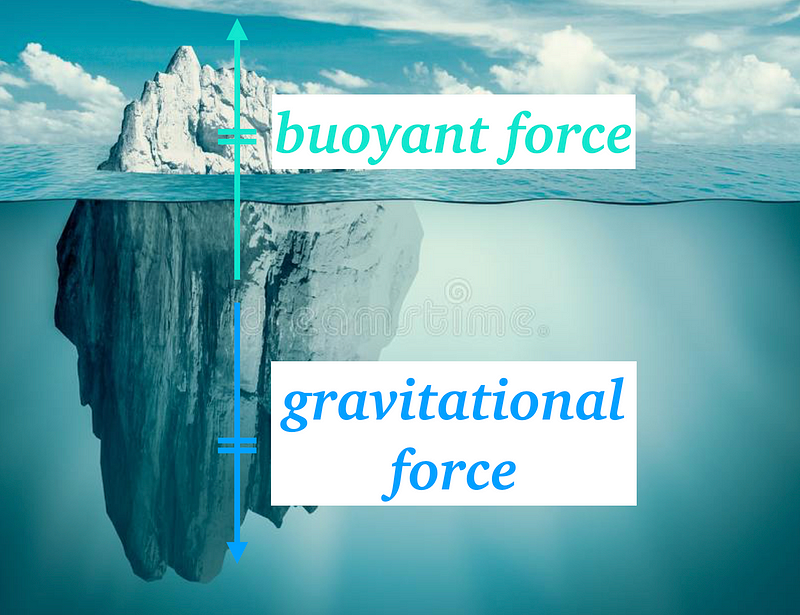
They consist of the gravitational force and the buoyant force:

(gravitational force) = (buoyant force).

The gravitational force can be calculated using the formula:

(mass) × (gravitational acceleration).

In this context, mass is given by (density) × (volume). Therefore, we can find the gravitational force on the iceberg as:

(density of ice) × (total volume of the iceberg) × (gravitational acceleration), which can be written as:

(gravitational force) = (density of ice) × (total volume of iceberg) × (gravitational acceleration) = ?_i × V × g.

Next, we must analyze the buoyant force acting upon the iceberg. According to Archimedes’ principle, the upward buoyant force exerted on a body immersed in a fluid, whether fully or partially, is equivalent to the weight of the displaced fluid.

So we can express:

(buoyant force) = (weight of the displaced fluid).

To determine the weight of the displaced fluid, we recall that:

(weight) = (mass) × (gravitational acceleration).

In this case, the weight of the displaced fluid equates to:

(mass of the seawater displaced by the iceberg) × (gravitational acceleration).

By substituting in our earlier definitions, we have:

(buoyant force) = (density of seawater) × (volume of seawater displaced) × (gravitational acceleration) = ?_s × v × g.

Since the gravitational force (?_i × V × g) and the buoyant force (?_s × v × g) are balanced, we can express this relationship as:

?_i × V × g = ?_s × v × g.

Now, let’s recap our findings. The proportion of the iceberg that remains above sea level is

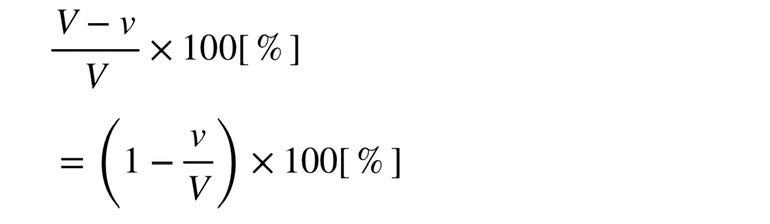
Our aim is to uncover the value of v/V. Using the equation derived above, we can determine v/V.

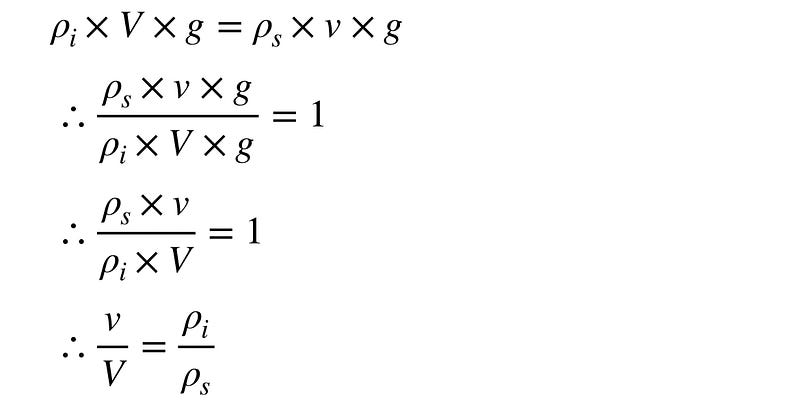
Substituting the density values, ?_i = 917 kg/m³ and ?_s = 1,024 kg/m³, we find:

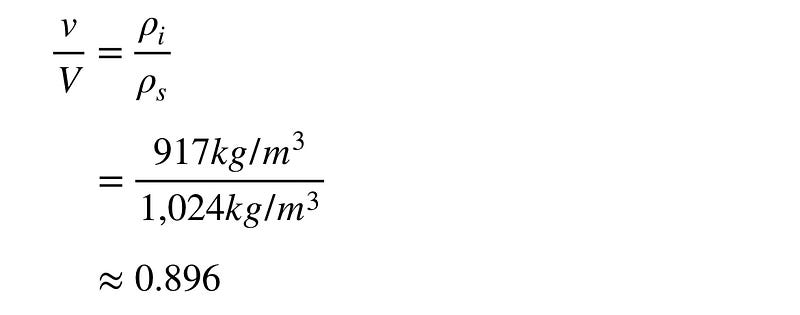
We conclude that v/V is approximately 0.896. By substituting this into the equation:

(1 - v/V) × 100 [%],

we find:

(1 - 0.896) × 100 [%] = 10.4 %.

The images of the iceberg presented above are credited to Satoshi Higashino.

SOCIAL:

Chapter 2: Exploring Iceberg Depths

This video titled "What's below the tip of the iceberg? - Camille Seaman" delves into the unseen aspects of icebergs, expanding on the scientific principles that illustrate their hidden depths.

In this informative video, "Percentage of Iceberg Submerged in Water," the focus is on the calculations and principles determining how much of an iceberg lies beneath the surface.