Exploring the Goldbach Conjecture Through Unique Perspectives
Written on
Chapter 1: Introduction to the Goldbach Conjecture
During my time studying mathematics, I often pondered over renowned unsolved problems as I drifted off to sleep. One night stands out vividly when I was captivated by the idea of representing the Goldbach conjecture using circles. Unsurprisingly, that evening yielded little sleep!
The Goldbach conjecture is one of the oldest and most notable unsolved enigmas in mathematics. Its origins trace back to a casual exchange between mathematicians Christian Goldbach and Leonhard Euler in 1742, although the concept had been acknowledged at least a century prior. This conjecture has since intrigued and challenged aspiring mathematicians, leading them into the depths of mathematical exploration.
In this brief article, we will delve into this problem by examining it from various perspectives, as this can sometimes spark new ideas for tackling it. Let’s first articulate the conjecture in its conventional form.
Section 1.1: The Traditional Formulation
The Goldbach conjecture asserts:
For every natural number n ≥ 2, there exist two prime numbers p and q such that 2n = p + q.
Alternatively, we express it as:
"Every even number greater than 2 is the sum of two primes."
Despite its straightforward formulation, proving it remains an incredibly challenging task. It feels like we require new methodologies to even begin our analysis. The conjecture has been verified for the first trillions of even numbers through computer calculations, yet we still face an infinite number of cases that remain untested, leaving us with a long journey ahead.

Section 1.2: Goldbach Circles
These circles were mentioned earlier. The concept is as follows: If a number 2n can be expressed as the sum of two primes p and q, then these primes must be equidistant from n on the number line. This means there exists an interval with prime endpoints and center n, which may have a length of 0 if n is itself prime. To visualize this, we can create a circle centered at n.
Definition:
A Goldbach circle centered at n ≥ 2 with radius r ≥ 0 is defined as either a circle that intersects two primes (for r > 0) or as a singular point if n is a prime number.
Here are some examples of the initial Goldbach circles.
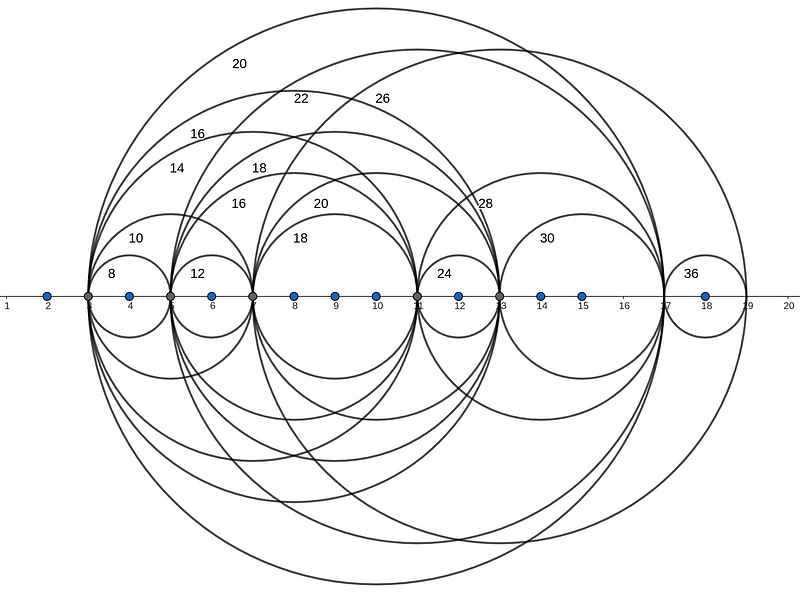
Several observations can be made regarding these circles. Firstly, concentric circles represent different Goldbach partitions; for instance, the two circles labeled 18 are concentric and illustrate the two distinct ways to express 18 as a sum of two primes: 18 = 11 + 7 = 13 + 5. Secondly, circles with a radius of r = 1 indicate twin primes (i.e., p and p + 2 are both primes). Lastly, if two circles intersect, then an additional circle exists at their intersection (a concept reminiscent of point-set topology).
We can rephrase the Goldbach conjecture in another manner:
Goldbach conjecture:
For every natural number n ≥ 2, a Goldbach circle centered at n exists.
Chapter 2: Goldbach Squares
I discovered a charming equivalence to the Goldbach conjecture years ago. Recall that a semiprime is defined as a number of the form pq, where both p and q are primes. Interestingly, the Goldbach conjecture can be equivalently stated as follows:
Goldbach conjecture:
For all natural numbers n ≥ 2, there exists an integer d such that 0 ≤ d < n-1, fulfilling n² - d² = pq.
In other words, for any number n, it is possible to find a non-negative integer d such that n² - d² results in a semiprime. To conceptualize this, imagine a large square composed of smaller cubes that you can rearrange however you wish. The larger square can either be represented solely as a 2D square shape and cannot transform into a 3D box, or you can remove a sub-square, leaving a shape that cannot be arranged into a 3D box but only into a 2D rectangle.

I will leave the proof of this equivalence as an exercise for the interested reader. Should you desire a hint, feel free to ask in the comments!
Section 2.1: Goldbach Lines
Consider the task of discovering the various Goldbach partitions of the number 42. One method is to write all numbers on the number line up to 21 and then "bend" the number line backward so the two lines overlap.
The illustration below clarifies this concept.
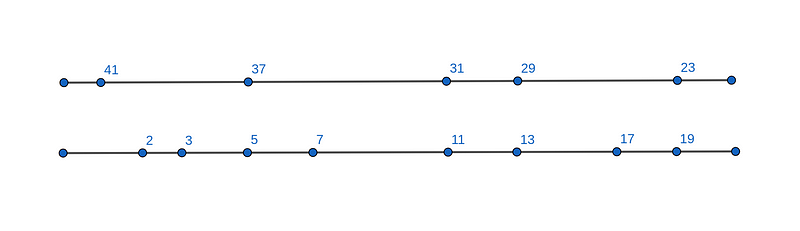
The lower line extends from 0 to 21, while the upper line progresses from 21 to 42 in reverse. The beauty lies in the fact that pairing numbers directly aligned above each other yields 42 for every such pair. Therefore, to find Goldbach partitions, we simply identify which primes align directly.
In this case, we observe that 42 = 5 + 37 = 11 + 31 = 13 + 29 = 19 + 23. This method elegantly showcases the symmetry that primes must maintain on both sides of n between 0 and 2n.
Section 2.2: The Goldbach Triangle
An alternative visualization of Goldbach partitions involves representing two copies of the number line on each face of an infinite isosceles triangle, drawing lines parallel to the opposite side through the primes.
The drawing below illustrates this concept.
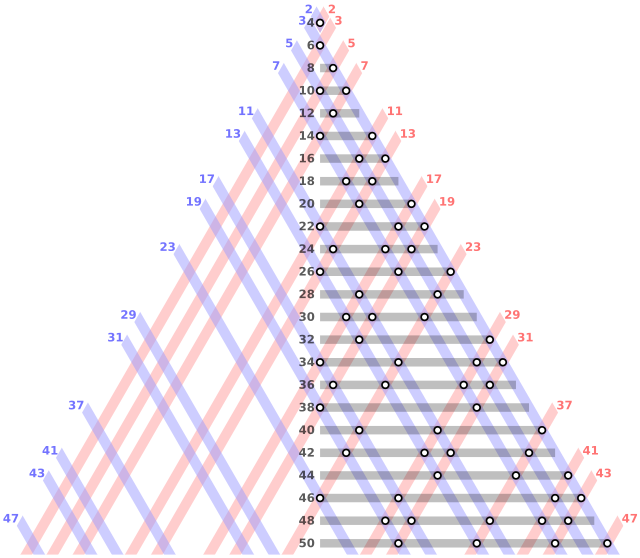
When two lines intersect, it signifies a Goldbach partition where the sum corresponds to the height from the triangle's apex.
Final Thoughts
In this concise article, I have projected this problem into various geometrically influenced realms. While I don’t anticipate that these formulations will simplify the problem, exploring it from multiple perspectives can enhance our understanding of the underlying mathematical entity. I refrained from discussing the circle method and other advanced tools to keep the article straightforward and visual, but traditional approaches exist for studying this problem.
What is your preferred formulation of the Goldbach conjecture? Do you have your own? If so, I would love to hear about it, so please reach out or leave a comment below. I’ll be sure to check them!
Thank you for reading.
If you enjoy articles like this one on Medium, consider getting a membership for full access. To join the community, simply click here.
The first video, "A Different Way to View Goldbach's Conjecture," offers a unique perspective on understanding this mathematical enigma.
The second video, "Goldbach Conjecture - Numberphile," provides insightful explanations and discussions surrounding this intriguing conjecture.