Today's Challenge

We'll utilize SymPy to compute various quantities in spherical coordinates, including the unit base vectors, the line element, the volume element, and the gradient.

Understanding the Unit Base Vectors

The base vectors corresponding to a given coordinate (curvilinear in our context) can be expressed mathematically. The initial step involves defining symbols for the coordinates, ensuring that we clarify which quantities are real and positive for cleaner results.

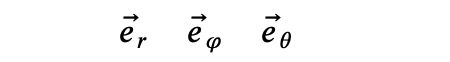
The transformation between Cartesian and spherical coordinates is crucial and can be represented as a dictionary.

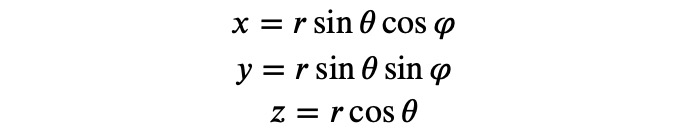
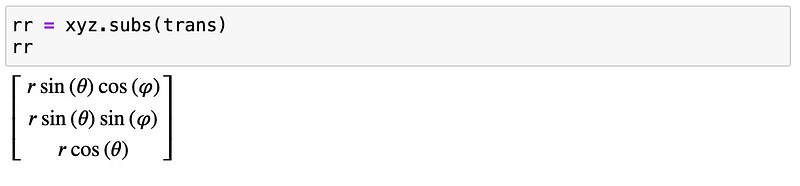
Next, we define the vector representation and convert it into spherical coordinates.

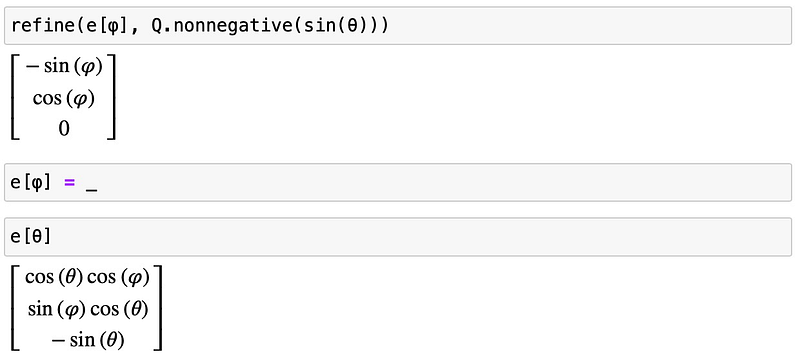
To obtain the unit base vectors, we normalize the base vectors and define helper functions for vector normalization:

We can explicitly use the assumption that certain angles are within specific ranges to refine our calculations:

Calculating the Line Element

Now, we can compute the line element, which is essential for various applications in physics and engineering.

Determining the Volume Element

To find the volume element, we need to remember that when transitioning between coordinate systems, the Jacobian determinant plays a vital role.

Computing the Gradient

Finally, we will calculate the gradient of a scalar function, which is a key concept in vector calculus.

The gradient is expressed in terms of the unit base vectors, and by applying the chain rule, we can derive the gradient in spherical coordinates:

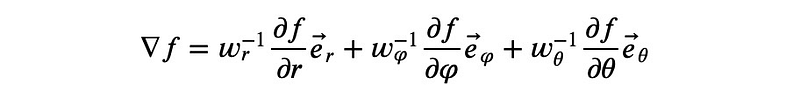
To visualize the concepts discussed, check out the following videos:

This video provides an overview of triple integrals in cylindrical and spherical coordinates, illustrating how to apply these concepts in practical scenarios.

This video demonstrates vector calculus using Python, covering important topics like gradient, divergence, curl, and Stokes' theorem, enhancing your understanding of vector fields.