Chapter 1: Introduction to Integral Calculus

This entry marks the third installment in the MIT Calculus Advanced Placement Test series. If you missed the earlier problems, be sure to check them out for a comprehensive understanding.

When tackling integrals that involve the multiplication of two or more functions, it's beneficial to identify any connections between them. Often, one function can be represented in terms of the derivative of another.

For example:

f(x) = x² + 3

f’(x) = 4x³

Recognizing this relationship allows us to utilize one of the fundamental techniques in integral calculus—u-substitution.

Section 1.1: Setting the Limits

At the specified points x = 0 and x = 1, we establish the following limits:

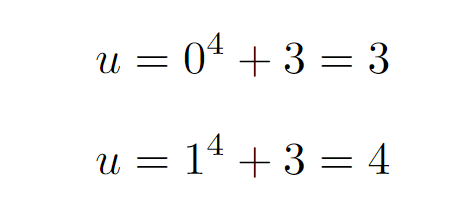
With this information, we can proceed to transform our integral accordingly.

Subsection 1.1.1: Transforming the Integral

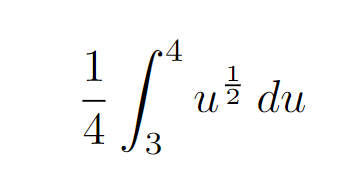
Take a moment to verify that this indeed represents the integral.

Next, we can apply the reverse product rule to determine the anti-derivative in terms of u.

Section 1.2: Finding the Anti-Derivative

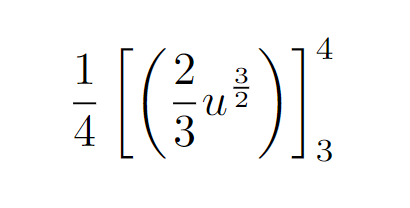
After substituting the limits, we arrive at the final solution.

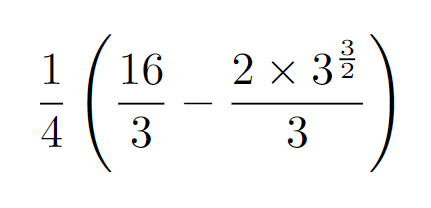
This is a fitting point to conclude our exploration.

What are your thoughts on this? Feel free to share in the comments below; I’m eager to hear your perspective!

Here's a video that provides insight into what a calculus test is like at MIT, as shared by a current student. It offers a glimpse into the expectations and challenges faced in this rigorous academic setting.

Additionally, this lecture on Single Variable Calculus from Fall 2007 at MIT provides foundational knowledge that aligns well with the concepts discussed here.

Math Puzzles: A Journey Through Mathematical Challenges

Explore an array of math puzzles spanning various topics including Algebra, Geometry, Calculus, and Number Theory. Share these with friends and challenge each other!

Thank you for reading! If you found this article insightful, don't hesitate to show your appreciation by clapping. Your support is invaluable!

If you feel inclined, consider buying me a coffee as a token of appreciation for my efforts in crafting these articles. Your generosity supports my writing and academic journey.