Chapter 1: Electric Potential and Its Zero Point

In many introductory physics textbooks, you will come across variations of two fundamental problems regarding electric charges. The first is identifying where the electric field equals zero, and the second is determining where the electric potential (relative to infinity) reaches zero. Although the electric field is a vector and the electric potential is a scalar, one might assume that the inquiry into potential would be simpler. However, this isn't necessarily the case. For a system with just two electric charges, the electric field vector can only be zero along the line that connects the two charges.

To better illustrate this, I’ll share a video that provides a visual explanation of how to locate the zero electric field.

Now, shifting our focus from the electric field, let’s delve into the more intricate topic of electric potential. This subject can be quite complex, and I'm still piecing together all the details. So, let's work through it together.

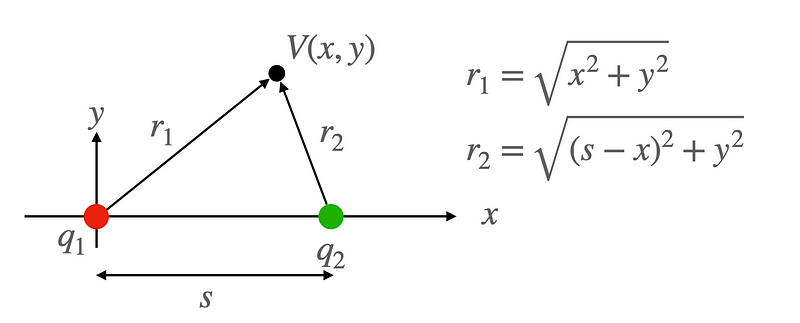
Imagine two charges, ( q_1 ) and ( q_2 ). I will position one charge at the origin and the other along the x-axis, as shown below.

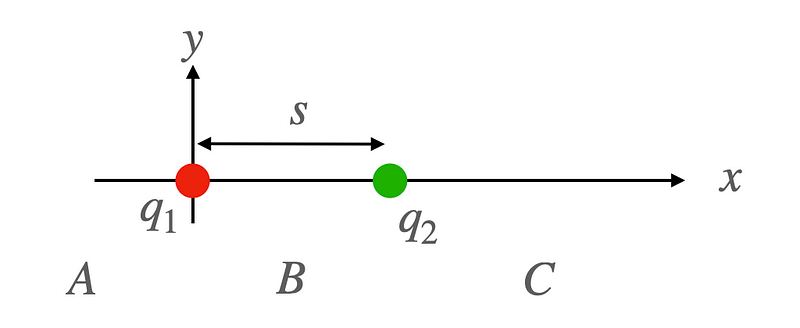
To find where the electric potential is zero along the x-axis, we first need to understand that the total electric potential at a point is the summation of potentials from each charge. It is important to clarify that this potential is referenced to infinity.

The potential ( V ) of a point charge can be expressed mathematically as follows:

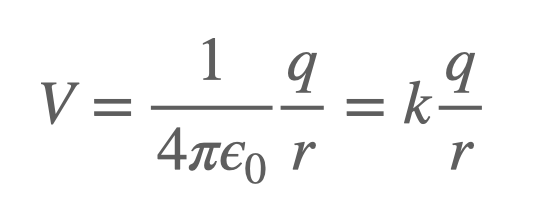
In this equation, ( k ) (or ( frac{1}{4pi epsilon_0} )) is a constant, ( q ) represents the charge, and ( r ) is the distance from the charge to the point where we want to measure the potential. For two charges, we will consider their vector positions, denoted as ( r_{q1} ) and ( r_{q2} ). The observation point where we want to find the potential will be labeled as ( r_{obs} ).

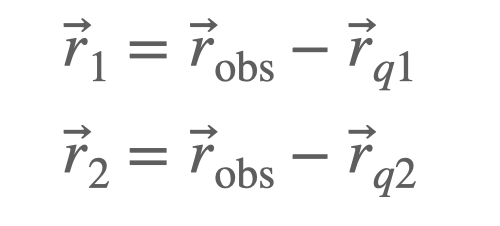
Once we determine the magnitudes of the vectors leading to the observation point, the total potential can be expressed as:

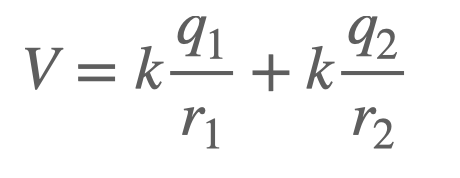
For now, we will concentrate on the x-axis. Let’s assume the observation point is at some position ( x ). This implies that ( r_1 ) equals ( x ) (since it's at the origin) and ( r_2 ) equals ( x - s ). Thus, we can express the potential as:

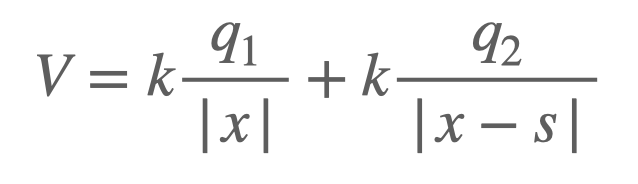
It's crucial to note that the absolute value of ( x ) must be considered, as the potential is dependent on the distance's magnitude. This indicates that the two charges must possess opposite signs; if both were positive (or negative), their potentials could not cancel each other to yield zero. Let’s assume ( q_1 ) is positive and ( q_2 ) is negative.

Next, we analyze the region to the right of ( q_2 ) (designated as region C). If we choose a point where ( x ) is greater than ( s ), the only scenario for the potential ( V ) to equate to zero is if ( q_2 ) has a smaller magnitude than ( q_1 ). This is because the denominator ( x - s ) will be lesser than ( x ) in this region. Let’s solve for ( x ):

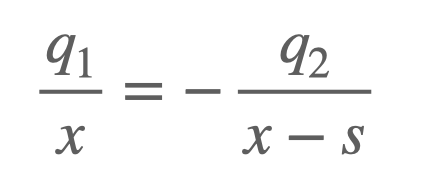
When we solve for ( x ):

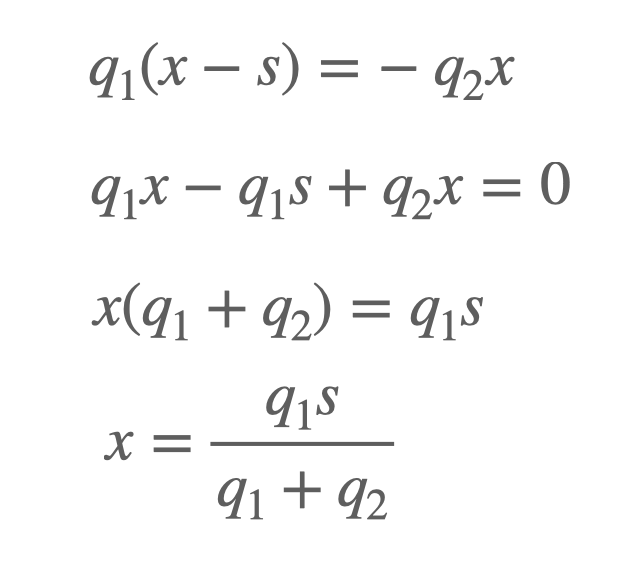
Assuming ( q_1 = 2 text{ nC} ) and ( q_2 = -1 text{ nC} ) with ( s = 0.1 text{ m} ), we find ( x = 0.2 text{ m} ) where the potential reaches zero.

Now, let's consider region B (between the two charges). We can express the total potential as:

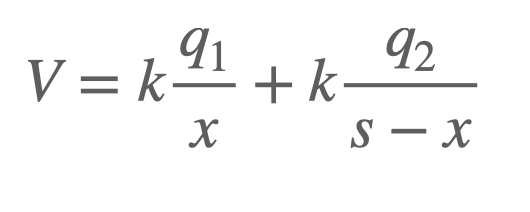
Solving for ( x ) here (without detailing every step, as it follows a similar method), we find:

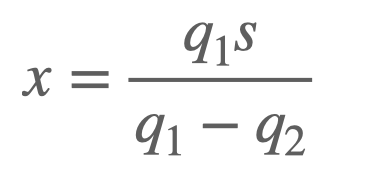
This assumes ( q_1 ) and ( q_2 ) are oppositely charged. Using the same values as before, we find another point of zero potential at ( x = 0.0667 text{ m} ), which is closer to the charge ( q_2 ) due to its smaller charge magnitude.

In region A, however, no position exists where the potential is zero. Since ( q_1 ) is greater than ( q_2 ), the potential from ( q_1 ) will always dominate in this area due to its proximity to any chosen ( x ) value.

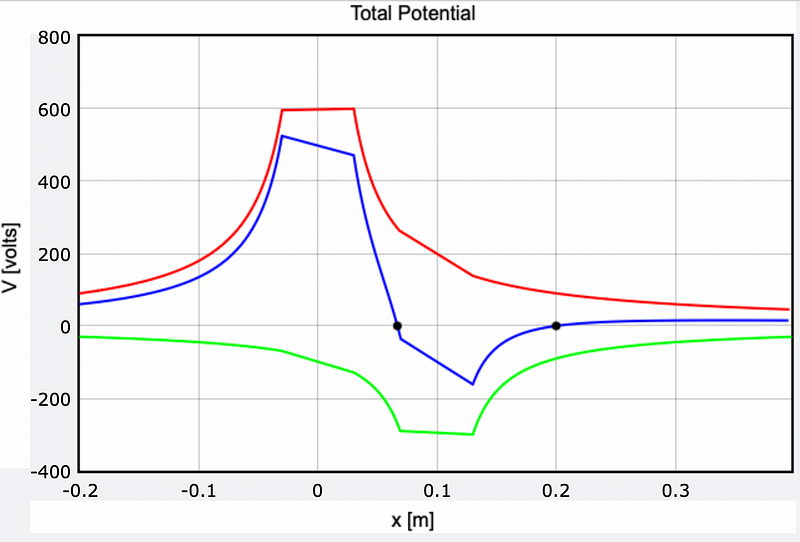
To visualize this further, here's a graph displaying the potential contributions from both charges, along with the total potential. The plot indicates where the potential is equal to zero.

Chapter 2: Exploring Other Locations for Zero Potential

But what if we look for zero potential points that are not restricted to the x-axis? Since electric potential is a scalar quantity, it can also cancel out at various locations, provided that the two potentials are equal in magnitude but opposite in sign. Let’s begin with region B (the area between the charges), illustrated below.

For the potential to be zero, the following must hold true (with ( k ) canceling out):

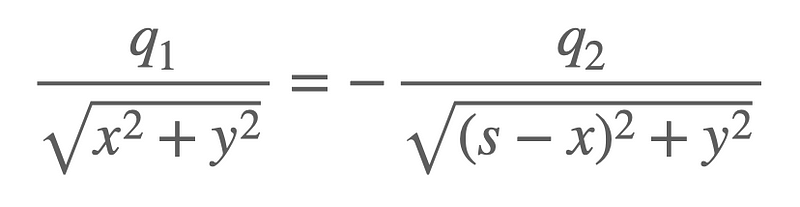
By squaring both sides and cross-multiplying (I know, it's a tedious process, but necessary):

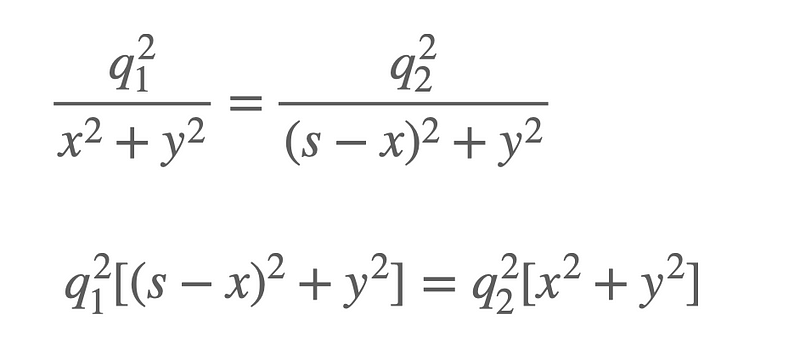
To simplify, I’ll divide both sides by ( q_1^2 ) and redefine a constant:

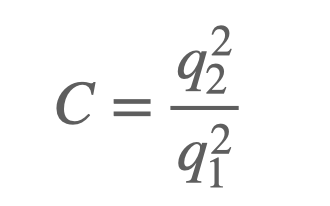
This new constant makes it easier to derive an expression for ( y^2 ):

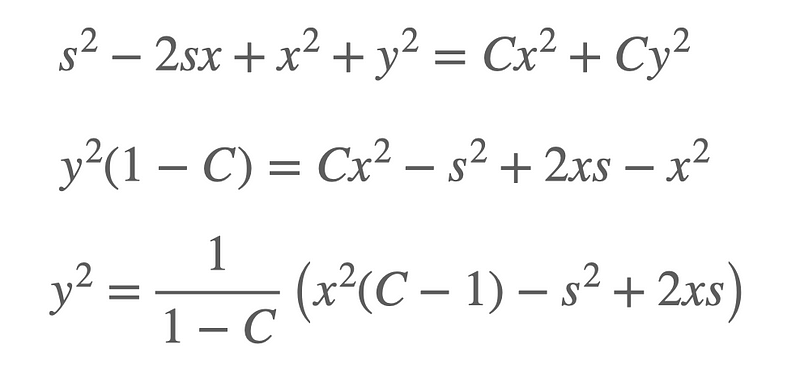
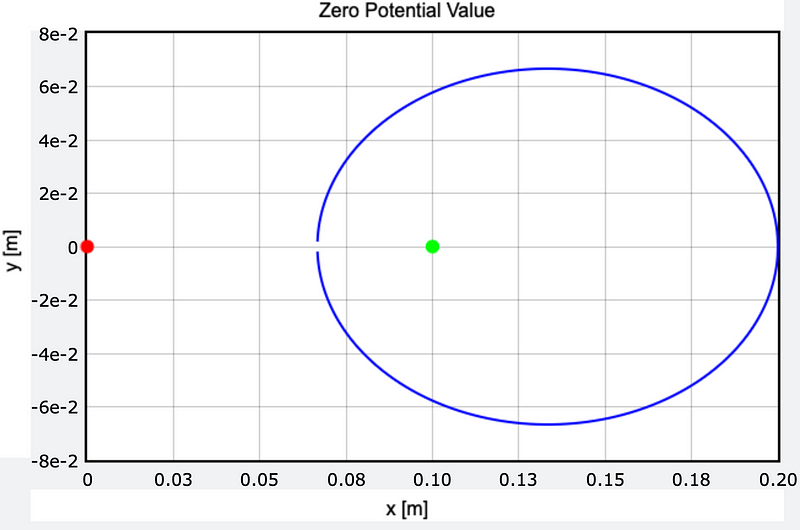
Here’s a segment of a plot showing some of these zero potential points, alongside the positions of the two charges.

That wraps up our exploration for now! But stay tuned, as I have additional insights to share about identifying these zero potential points in future discussions.