How Evidence Operates

Consider a theoretical scenario where 5 out of every 100 individuals (5%) are infected with COVID-19. In this context, a testing device is available, boasting specific accuracy metrics: when 1,000 COVID-19 patients are tested, 900 yield positive results (90% accuracy). However, among 1,000 healthy individuals, 100 (10%) will also receive a positive test result despite not being infected.

Now, if a woman tests positive, what is the likelihood that she actually has COVID-19?

At first glance, one might assume the probability stands at 90%, given that 900 out of 1,000 infected individuals test positive. However, it's essential to remember that only 5% of the population is infected.

Let's examine a sample of 2,000 individuals from this hypothetical world. Based on our initial assumption, 100 individuals are expected to be infected. Out of these, 90 will test positive. Conversely, from the remaining 1,900 healthy individuals, 190 will also test positive. Thus, we have 280 positive tests out of 2,000 individuals—of which only 90 are actual cases of COVID-19.

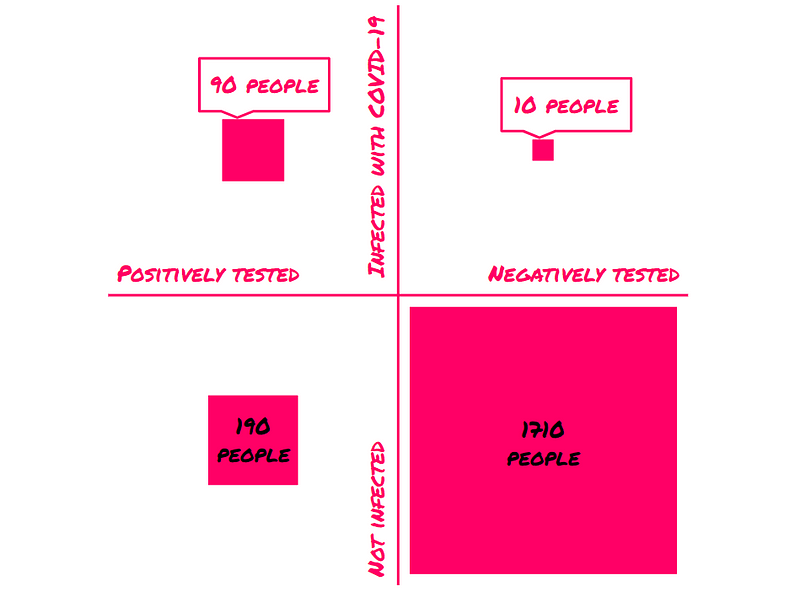
From this analysis, it's clear that if 280 individuals test positive, only 90 of them genuinely have the virus, which means the woman who tested positive has about a 32% (90 / 280 * 100 ≈ 32.14%) chance of being infected.

You may find this counterintuitive, given that the device correctly identifies 90% of COVID-19 cases. However, it also inaccurately identifies 10% of healthy individuals as positive, which affects the overall probability. The larger number of healthy individuals skews the results, as they outnumber the infected by nearly 19 times.

Thus, when we question how many infected individuals are among those who tested positive, we uncover a relatively small fraction of true cases. Even though the 32% might seem low, consider this: without a positive test, the probability of having COVID-19 is merely 5%—the device significantly improves our odds.

How Eve Makes Her Choice

Now, let's link this back to Eve's decision-making process. When Omega asserts his remarkable predictive abilities in Newcomb’s Problem, Eve is naturally skeptical; after all, such claims can seem implausible. Nevertheless, Omega's assertion might hold merit, and Eve assigns a 10% probability to the notion that "Omega predicts perfectly."

Upon witnessing Omega's accurate prediction, Eve should recognize this as some evidence supporting Omega's claim, albeit not overwhelmingly compelling; a single correct prediction holds little weight if random predictions can produce similar results.

To gauge how much her initial 10% probability should be adjusted, we can model this scenario similarly to the COVID-19 analysis.

Imagine a group of 2,000 people engaged in Newcomb’s Problem. With a prior probability of 10% that Omega can predict perfectly, we anticipate 200 individuals receiving accurate predictions. The remaining 1,800 participants will receive random predictions, of which 50% will be correct—resulting in another 900 accurate predictions and 900 incorrect ones.

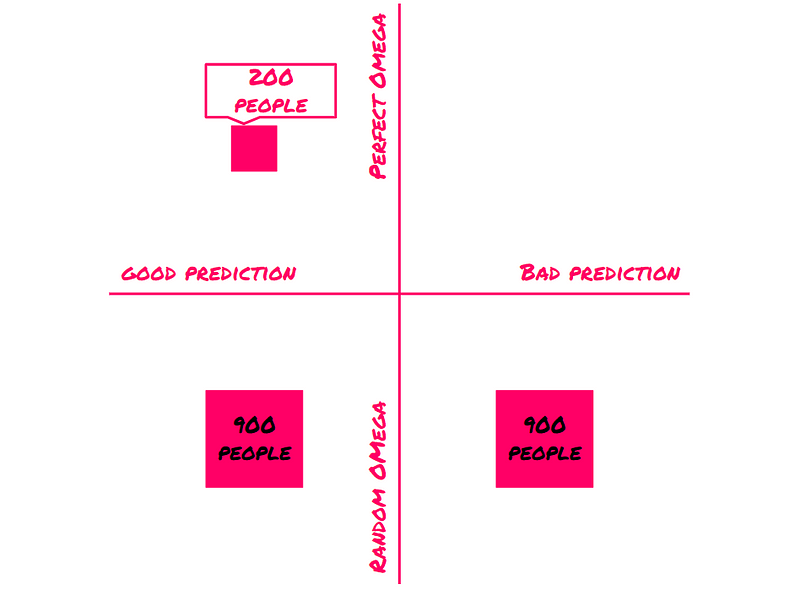
In total, this means 1,100 individuals received good predictions, of which 200 were accurate due to a perfect Omega. That results in an approximate 18% probability of Omega's perfection—a significant increase from Eve's original belief, but she remains doubtful.

As Eve observes a second successful prediction, she recognizes that a randomly predicting Omega has a 25% chance of generating two correct predictions in a row. In contrast, a perfect Omega will always predict accurately.

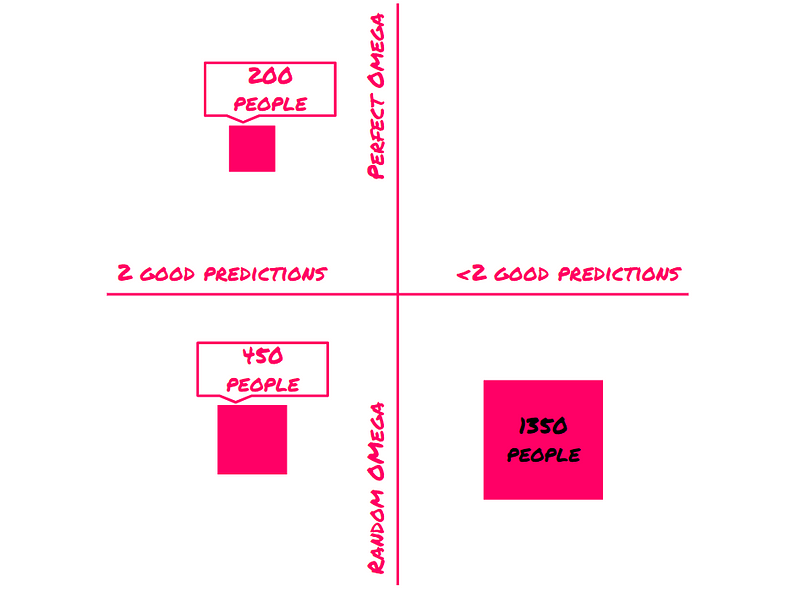
Thus, as Eve witnesses more correct predictions, her confidence in Omega's abilities grows stronger.

After about ten correct predictions, Eve becomes quite certain that Omega is indeed capable of perfect predictions. However, this realization also implies that if she opts to two-box, it serves as evidence that Omega anticipated her choice. Conversely, choosing to one-box indicates to Omega that she will one-box, suggesting that Box B will contain the $1,000,000.

Consequently, Eve's decision to one-box aligns with Evidential Decision Theory (EDT), which posits that one should choose the action that best indicates a favorable outcome. In this context, two-boxing correlates with receiving only $1,000, while one-boxing suggests the possibility of acquiring $1,000,000. Hence, EDT endorses Eve's decision to one-box.

However, is this reasoning sound? While I argue that one-boxing is indeed the appropriate choice in Newcomb's Problem, EDT's rationale is flawed; it mistakenly equates correlation with causation.

Understanding Correlation vs. Causation

Let's explore a hypothetical scenario where, similar to our reality, smoking is closely linked to lung cancer. However, in this case, smoking does not directly cause lung cancer. Instead, a genetic predisposition exists within a segment of the population that leads to both a preference for smoking and a higher risk of lung cancer. When controlling for this genetic factor, the correlation between smoking and lung cancer disappears.

Consider your preferences in this situation:

1. Smoking, but avoiding lung cancer
2. Not smoking, while avoiding lung cancer
3. Smoking, and developing lung cancer
4. Not smoking, and developing lung cancer

Should you smoke in this scenario? The answer is yes. Your enjoyment of smoking outweighs the potential lung cancer risk, as smoking does not affect your likelihood of developing cancer—this is determined solely by the genetic factor.

What would Eve, adhering to EDT, conclude? Unfortunately, due to the correlation between smoking and lung cancer, she would mistakenly perceive smoking as indicative of lung cancer risk. The following illustration depicts this relationship:

As Eve observes more cases, the proportion of smokers developing lung cancer will appear to increase. However, she fails to understand that while smoking correlates with lung cancer, it does not directly cause it. The real cause lies within the genetic lesion, which also predisposes individuals to smoke.

We can also analyze this issue in terms of the subpopulations with and without the lesion. In both instances, smoking does not serve as evidence for lung cancer—this correlation only exists when considering the entire population.

In this example, of the 1,200 smokers, 520 have lung cancer, while of the 1,200 non-smokers, 200 are diagnosed with lung cancer. Although there appears to be a strong correlation between smoking and lung cancer, within the subsets of those with and without the lesion, no such correlation exists.

Consequently, evidence-based decision-making appears to be flawed due to a fundamental misunderstanding: the confusion of correlation with causation. If we focus solely on the causal effects of our choices, we would choose to smoke in the Smoking Lesion scenario.

Next, we will explore Causal Decision Theory, which addresses these nuances. Thank you for reading!

If you wish to support Street Science, please consider contributing on Patreon.