Can You Solve This Fascinating Japanese Sangaku Geometry Puzzle?
Written on
Chapter 1: Introduction to Japanese Sangaku
Today's mathematical challenge is a captivating Japanese Sangaku puzzle. These geometrical problems were traditionally etched on wooden tablets and offered at Shinto shrines or Buddhist temples during Japan's Edo period, engaging individuals from various social backgrounds.
In this puzzle, your task is to determine the fraction of the outer circle that is filled by the yellow, red, and blue circles. As a hint, remember that a circle comprises four quadrants.
I encourage you to take a moment, grab some paper and a pencil, and give it a try. Once you're ready, continue reading for the solution!
Solution
Let's start by focusing on the upper left quadrant of the circle. We will denote the radii of the yellow, blue, and red circles as 1, R, and r, respectively, simplifying our calculations by assigning the yellow circle a radius of 1.
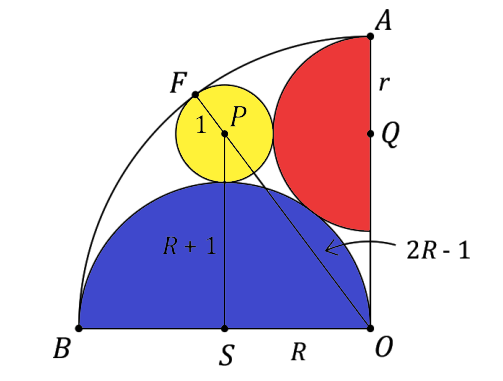
Examining triangle OPS, we find the hypotenuse OP corresponds to the length OF - PF. Here, OF represents the diameter of the blue circle, which is calculated as 2R. Therefore, we have OP = 2R - 1.
Moreover, PS equals the sum of the radii of the yellow and blue circles, giving us PS = R + 1, while SO is simply R. With this information, we can utilize the Pythagorean theorem on the right triangle OPS.
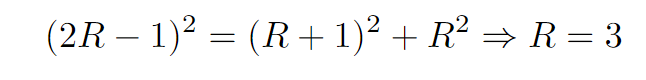
Through our calculations, we discover that the radius of the blue circle is 3.

Next, we will analyze another triangle OQS by connecting points Q and S to form its hypotenuse.
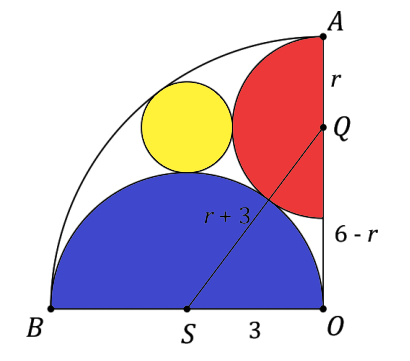
In this case, QS is the total of the blue and red radii, which is expressed as r + 3. QO, on the other hand, is calculated as the blue diameter minus the red radius, yielding 2(3) - r = 6 - r. The base SO is simply the length of the blue radius, which is 3. Once again, we can apply the Pythagorean theorem.
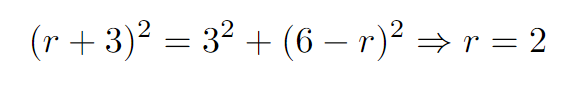
From our analysis, we determine that the radius of the red circle is 2.
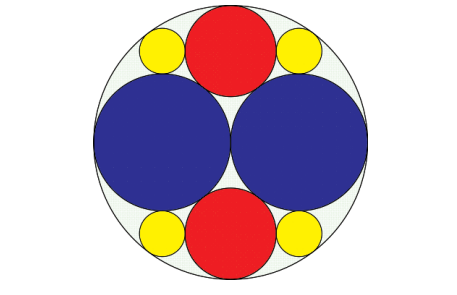
Now that we have established the radii of the circles as 1, 2, and 3, we can note that the outer circle's radius is the diameter of the blue circle, which measures 6.
In total, there are 2 blue circles, 2 red circles, and 4 yellow circles present. Consequently, the fraction of the outer circle that is occupied by these eight inner circles is calculated as follows:
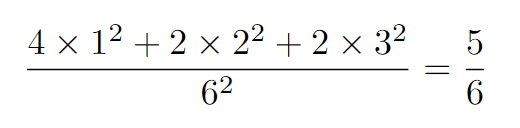
Remarkably, pi is not considered in this calculation since it cancels out!
What were your thoughts during this process? I would love to hear your insights in the comments below!
Don't forget to share this collection of intriguing math puzzles with friends and family.
Math Puzzles
Explore a variety of math puzzles, including Algebra, Geometry, Calculus, and Number Theory. Share this with your network!
Chapter 2: Video Insights on Japanese Sangaku
In the first video, titled "A Japanese Temple Problem, a Sangaku," viewers can dive deeper into the intricacies of Sangaku puzzles and their historical significance.
The second video, "An Easy Sangaku Puzzle (Japanese Temple Problem)," provides a straightforward approach to solving these engaging challenges.
Thank you for taking the time to read this! If you found this article helpful, please show your support by clapping.

If you enjoyed this piece, consider treating me to a coffee! Additionally, feel free to reach out if you would like a customized math puzzle article.
With gratitude, Bella