A Physics Exploration: The Feasibility of Human Sling Shots
Written on
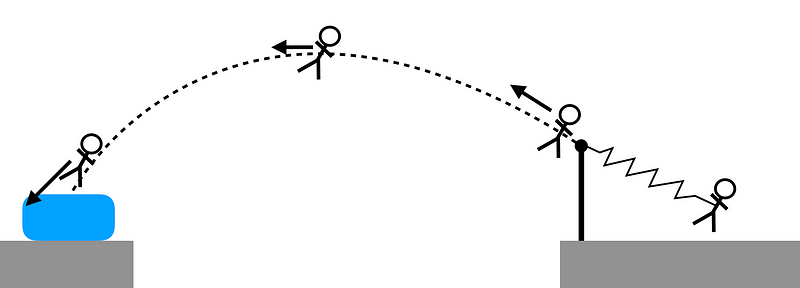
Have you ever explored the vastness of "The Internet"? If so, you might have stumbled upon a plethora of videos showcasing various stunts—some are outrageous, some are genuine, and others are complete fabrications.
One such video features an individual in a massive slingshot perched atop a building, launching into the air towards another structure equipped with a large net for landing. While it appears thrilling, it’s important to note that this video is a fabrication from an older advertisement.
Just because we recognize its falsity doesn’t preclude us from applying some physics to the scenario. If this were a real occurrence, I doubt it would be effective; even a minor alteration in launch velocity could result in the individual missing the net entirely.
This situation raises several intriguing physics questions: - What launch speed is necessary to reach the adjacent building? - How can we estimate the spring constant of the slingshot? - What acceleration would a person experience during the launch, and would it be safe? - How would the landing acceleration compare? - Can we disregard air resistance in this scenario? - If there were slight variations in the launch angle, how frequently would the individual miss the target? - What would the cost of such a launch be, and what might the insurance policy entail? - Lastly, if someone undertakes this and survives, do they receive a commemorative t-shirt?
I won't answer all of these questions, but I will help you begin the exploration—consider the rest as your homework.
Estimating Launch Speed
Let’s set aside the mechanics of the launcher for a moment. Once the individual is airborne, how fast must they travel to reach the other building? I will begin with the following assumptions: - The launch angle is approximately 35 degrees. - Air resistance is negligible. - The launch and landing points are at equal heights. - The distance between the buildings is 450 meters (as determined via Google Maps, using structures across from each other in Dubai Marina).
This sets us up for a straightforward projectile motion problem. In the absence of air resistance, we have two distinct components: horizontal motion with constant velocity (no horizontal forces acting) and vertical motion with a constant acceleration of -9.8 m/s² (due to gravity). These motions are independent, except for the shared time duration.
Applying basic kinematic equations allows us to analyze both horizontal (x) and vertical (y) movements.
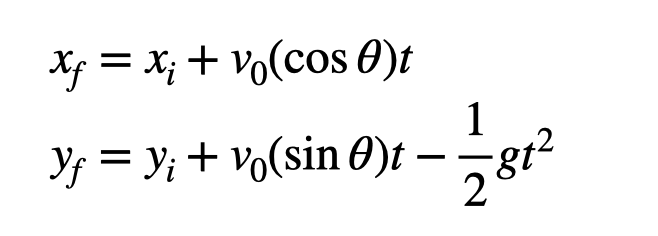
We can select our coordinate system and time reference. It’s logical to position the origin at the launch point, meaning x_i = 0 meters and y_i = 0 meters. Additionally, I will begin the timing at the launch point so that the time measured will correspond to the final position.
For the endpoint, we know x_f is 450 meters, and the final y-position also equals 0 meters (assuming the launch and landing occur at the same elevation). This simplifies our equations significantly.
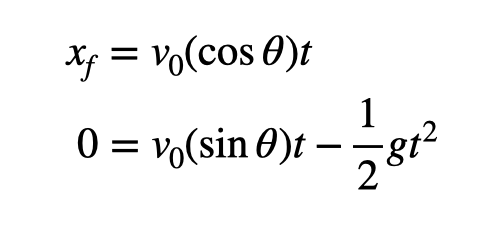
Now, I can manipulate the first equation to find time (t) and then substitute that into the second equation to determine the initial velocity (v_0). Notice how the time in the first equation cancels with the t² term.
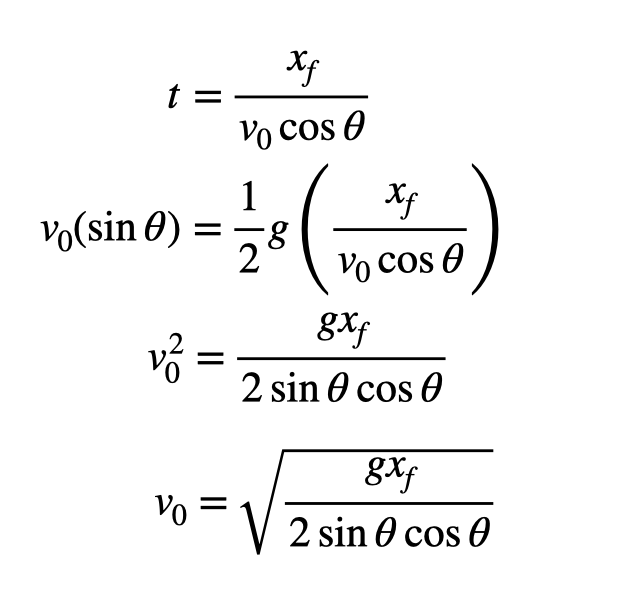
Inserting our values, I calculate the necessary launch speed to be 68.5 meters per second (about 153 mph).
Bungee Spring Constant
Next, we need to determine the spring constant of the bungee cord used for launching. I’ll begin with several assumptions: - The bungee cord follows Hooke’s law, meaning the force it generates is directly proportional to its extension. - The bungee has an unstretched length of zero meters. - The bungee stretches 10 meters, and the combined mass of the person and chair is 100 kg. - The change in gravitational potential energy is minor compared to the change in spring potential energy (allowing us to disregard any upward motion).
This sets us up to apply the work-energy principle.
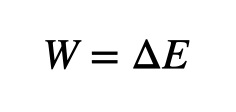
This principle states that the work performed on a system equals the change in energy within that system. For our analysis, let’s define our system as the individual (plus chair) and the spring (bungee). Once released, no external force acts on this system, indicating that the changes in kinetic energy (of the person) and spring potential energy must sum to zero.
We can represent kinetic and potential energy as follows:
In this case, the potential energy is defined by the stretch or compression of the spring (s). The work-energy equation can then be expressed as:
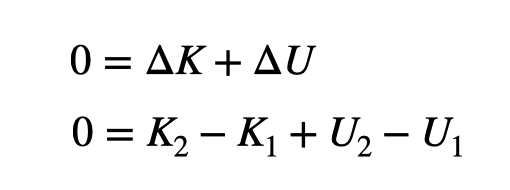
Two terms in this equation equal zero: the initial kinetic energy is zero since the person starts from rest, and the final potential energy also equals zero once the spring is unstretched. Thus, we have:
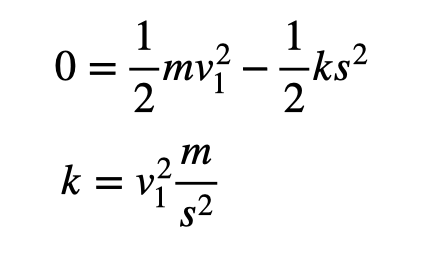
Substituting in the values for initial velocity, mass, and stretch reveals a spring constant of 4693 Newtons per meter. This is a relatively high spring constant for a bungee, but given our context, we recognize this is a fictional scenario.
Acceleration During Launch
Experiencing extreme accelerations can be detrimental to humans. For instance, when someone falls and abruptly halts upon hitting the ground, they transition from a downward velocity to zero almost instantaneously—painful, to say the least. Fortunately, research provides insights into the maximum tolerable acceleration (measured in g's) for humans.
Referencing a plot from Wikipedia:
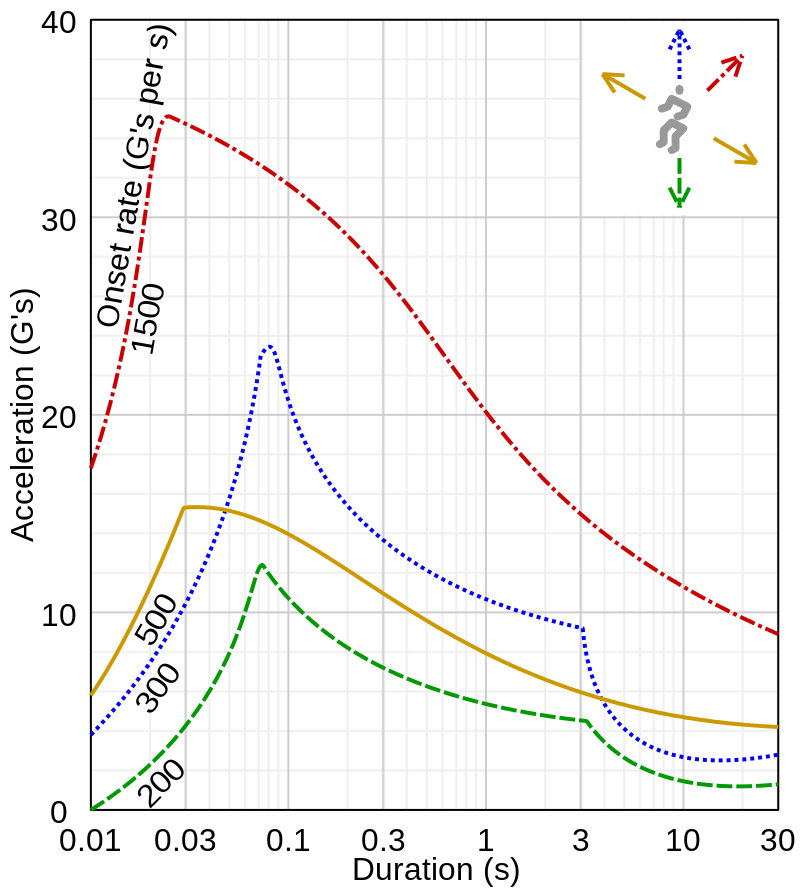
In the case of our bungee-launching individual, they could endure around 35 g's for a very brief period (approximately 343 m/s²). We must now assess whether their calculated acceleration exceeds this threshold. I’ll apply two different methods to evaluate this.
The first approach utilizes the spring constant. Immediately after the bungee is released, the spring force is k*s (neglecting the minor gravitational force). If this is the only force acting, it equals m*a (Fnet = ma), leading to an acceleration of:
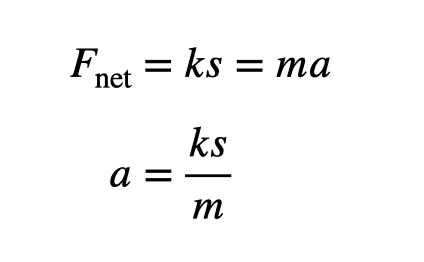
Substituting in values yields an acceleration of 469 m/s²—quite high. As the individual progresses along the launch path, this value decreases, with the average acceleration approximating 235 m/s² (still concerning).
The second method involves analyzing the video itself. By using Tracker Video Analysis, I can assess the individual’s motion. Ideally, I’d generate a position vs. time plot, but the video angle isn’t ideal. Instead, I’ll focus on the time aspect. The launch duration from the video is 0.267 seconds. Given the speed of 68.5 m/s (from previous calculations), I can compute the average acceleration.
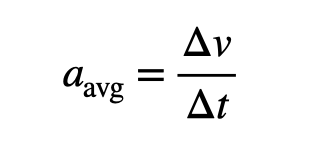
Using this method reveals an average acceleration of 257 m/s². It's surprising how closely the two methods yield similar results; perhaps the video holds more truth than initially thought.
Considering Air Resistance
Is it justifiable to overlook air resistance? Let's compare human trajectories with and without factoring in air resistance. The interaction between a human and the air can be modeled as follows:
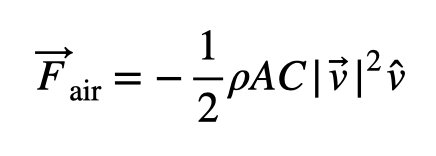
In this model, ? represents air density, A denotes surface area, and C is the drag coefficient. A critical aspect of this scenario is that the vector force opposes the velocity and is dependent on its magnitude. This complexity makes determining the trajectory challenging. However, numerical calculations simplify the task. For further understanding, here’s a video explanation.
One challenge in this calculation is determining values for both A and C for a human. However, we can derive the product AC. I know that a skydiver reaches terminal velocity at 120 mph (54 m/s). At this speed, the drag and gravitational forces balance, allowing us to calculate AC easily.
Now, here’s a plot illustrating two individuals with identical initial velocities. The blue curve represents motion without air resistance, while the red curve accounts for it. Here’s the code if you wish to explore it further.
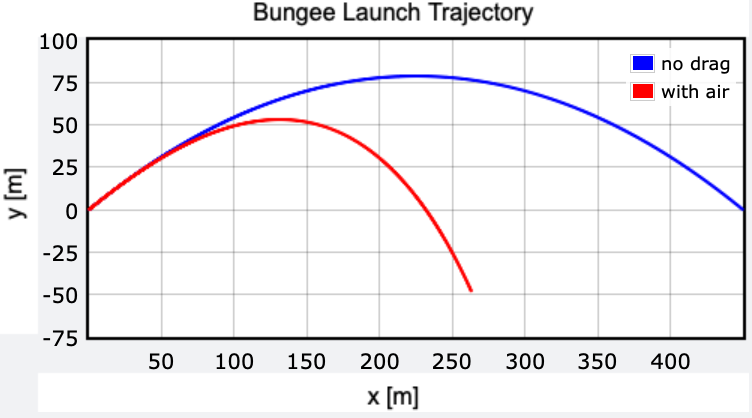
Indeed, air resistance significantly impacts the motion. The no-drag launch speed exceeded terminal velocity, proving that it cannot be ignored.
So, what launch speed would actually be necessary for a human? This can be easily determined by rerunning my Python code with varying initial velocities until achieving a final position of 450 meters. The result is a required launch speed of 146.5 m/s, considerably higher than before.
Homework Assignment
Now it’s time for your homework. Yes, it will be evaluated. Please refrain from cheating or using ChatGPT. - Recalculate the spring constant and acceleration considering the launch speed adjusted for air resistance. - The estimated launch time with air resistance is 10 seconds, but the video shows around 6 seconds. By altering the launch angle (to something other than 35 degrees), can you reconcile the timings? - If the slingshot launch cart is retracted 5 centimeters to the side, introducing a slight lateral velocity component, will the individual still land on the net? - At the video’s conclusion, the individual lands in a pool. Estimate the pool’s depth required for a safe (or relatively safe) landing.