# How Much String Is Needed to Encircle the Earth? A Surprising Puzzle
Written on
Chapter 1: Introduction to the Puzzle
Have you ever wondered how much string it would take to encircle the Earth? This seemingly monumental task is actually a gateway to a thought-provoking mathematical puzzle that sheds light on intriguing aspects of human behavior.
To kick things off, I will provide a brief overview of this puzzle. Following that, I will delve into an analysis of the behavioral patterns it reveals. Finally, I will clarify the reasoning behind the solution.
By the end of this article, you should acquire insights that allow you to connect this puzzle to similar real-world scenarios, which may help you make more informed decisions in analogous situations.
Section 1.1: The Initial Question
Let’s begin with a straightforward question: How much string is required to wrap around the Earth at the equator? To solve this, we can assume the Earth is a perfect sphere and focus on measuring its circumference. This measurement will indicate the length of string needed.

Assuming the Earth's circumference at the equator is approximately 40,000 kilometers (km), you would need a string of that same length. However, this initial calculation is just a warm-up—there are no rewards for simply getting it right.
Section 1.2: The Next Challenge
Now, suppose I ask you to wrap the Earth again, but this time with a second piece of string that floats 1 centimeter (cm) above the surface. Again, we’ll consider the Earth as a perfect sphere.
The question is: How much longer does this second string need to be compared to the first? You don’t need to provide an exact number; just keep your rough estimate in mind.
Chapter 2: A Twist with a Basketball
Now let's scale things down. Imagine you have a perfectly spherical basketball with a circumference of 24 cm. Your task is similar: wrap the basketball with a piece of string around its equator.
Since the basketball's circumference is 24 cm, the string will also measure 24 cm. Then, you will need to wrap a second piece of string that hovers 1 cm above the basketball’s surface.
The question remains: How much longer must this second string be than the first to maintain that height? Again, just keep your thoughts on this question handy as we move on to the answers.
Section 2.1: The Surprising Answers
For the Earth, the second string must be about 6.28 cm longer than the first to hover 1 cm above the surface. Surprising, isn’t it? Did you manage to guess this number?
Similarly, for the basketball, the second string also requires an additional length of around 6.28 cm to achieve the same hovering effect. Fascinatingly, both scenarios yield the same result. Were you expecting this?
Section 2.2: Understanding the Anchoring Effect
Most individuals would intuitively assume that the answer for the Earth would be substantially larger, while the answer for the basketball would be significantly smaller. This phenomenon can be attributed to the anchoring effect.
This cognitive bias occurs when our decisions are influenced by specific reference points or figures we encounter in a particular context. In the case of the Earth, the significant number—40,000 km—leads us to overestimate the answer, whereas the smaller circumference of the basketball (24 cm) leads to a lower estimation.
This process often happens without our conscious awareness, illustrating the power of cognitive biases.
The first video, "Wrapping a Rope around the Earth Puzzle (TANTON Mathematics)," explores this fascinating puzzle in greater detail.
The second video, "Rope Around the Earth | #1minutemaths | Mathematigals," provides additional insights and visualizations related to this concept.
Section 2.3: The Logic Behind the Puzzle
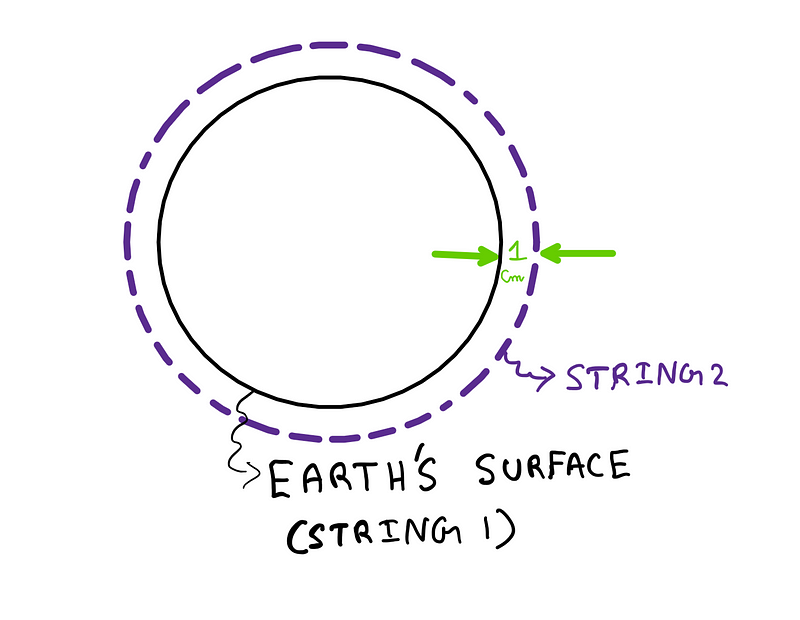
To truly grasp this puzzle, it’s essential to recognize that we are dealing with circumferences. The formula for circumference is given by 2πR, where R represents the radius.
When the second string hovers 1 cm above the Earth’s surface, its radius increases by 1 cm. The length of the second string can be calculated as follows:
[Circumference of Second String] — [Circumference of First String] = [2π(R + 1 cm)] — [2π(R)] = 2π[(R + 1 cm) — R] = 2π(1 cm) ≈ 6.28 cm
This same reasoning applies to the basketball, where the difference in radii is also 1 cm, leading to the same result.
Final Thoughts
Though this puzzle appears simple, it conveys a significant lesson. When making important numerical or financial decisions, it’s beneficial to set aside gut feelings and instead engage in thorough calculations.
While it may feel tedious at the moment, this approach often leads to a clearer understanding of the issue at hand. We might not gain much from physically wrapping strings around the Earth, but understanding how to tackle real-life problems is always a valuable skill.
I hope you found this article both interesting and informative. If you’d like to support my work as an author, consider clapping, following, and subscribing.
For further exploration, you might enjoy reading "How To Use Science To Win At Rock-Paper-Scissors?" and "What Really Happens When You Divide By Zero?"