The Fascinating Truth About Imaginary Numbers in Mathematics
Written on
Chapter 1: Unveiling the Mystery of Imaginary Numbers
In the realm of mathematics, there's a remarkable revelation: by tackling one seemingly impossible equation, we unlock solutions to all algebraic equations.
From our early algebra studies, we know that the square of any real number yields a positive outcome. Consequently, the equation
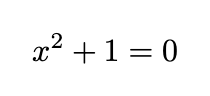
appears to lack a solution. Should we abandon hope? Not at all! Mathematics thrives on creativity, allowing us to introduce a new solution, denoted as i, so that
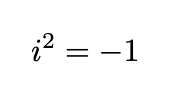
This imaginary unit possesses extraordinary capabilities. By permitting it to resolve this elementary equation, we gain the ability to solve all algebraic equations tied to any polynomials—and even more extensive classes of functions. This potential is unleashed through the profound relationship between algebra and geometry, facilitated by complex numbers.
Factoring Distance
One of the first insights comes from reevaluating the concept of distance (or its square). Picture this: I walk 3 meters forward and 4 meters sideways. What distance have I covered? The answer, which is 5 meters, stems from the Pythagorean theorem, as illustrated by 5² = 3² + 4². More generally, we arrive at the well-known formula:
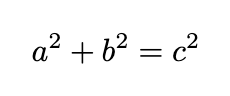
What does the imaginary unit i contribute to this? The answer lies in factorization. There exists a familiar formula (a + b)(a - b) = a² - b², but it requires a minor adjustment when compared to the Pythagorean formula. We can amend this using i:
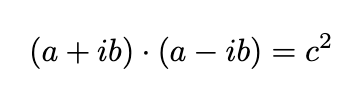
The importance of this observation is that the intricate notion of distance simplifies into a basic algebraic idea of multiplication. This technique can also be employed to factor differential operators.
Complex Numbers
The geometric connection illustrated above allows us to define an abstract entity known as the complex number: essentially anything represented in the form a + ib. For example, my movement of 3 meters forward and 4 meters sideways can be captured as z = 3 + i4.
However, symbols alone lack significance. Their value emerges from the engaging operations we can perform with them. For complex numbers, we can easily comprehend addition, subtraction, and multiplication. The missing component is division.
Fortunately, our connection to the Pythagorean formula assists us; we can define division through multiplication.
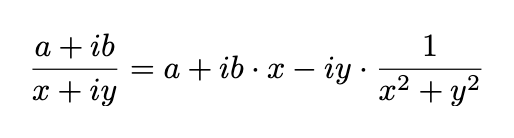
This definition aligns with division in real numbers, making equations such as those below meaningful:
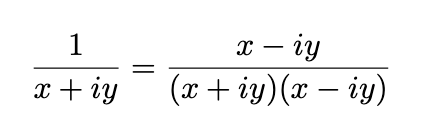
What is the significance of this intricate framework? It turns out that this allows us to solve not just the initial equation x² + 1 = 0 but all algebraic equations.
Solutions for All Algebraic Equations
The Fundamental Theorem of Algebra states that equations of the form:
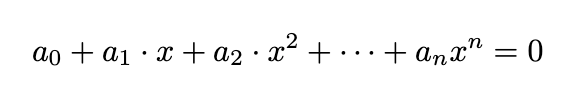
will always guarantee at least one solution expressed as x = a + ib. This is truly remarkable, as it indicates that by resolving one impossible equation x² + 1 = 0, we pave the way for solutions to all polynomial equations of this form. Thus, the theorem implies that complex numbers, rather than real numbers, serve as the most natural foundation for these algebraic equations.
Various proofs exist for this theorem, and I will outline some intuitive explanations. We begin with the function
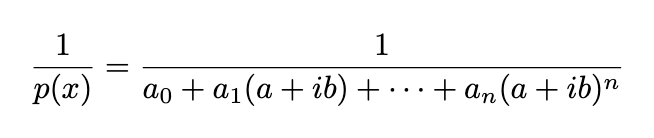
This function satisfies the differential equation below (by applying the chain rule and disregarding all potential singularities):
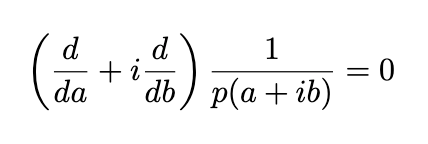
This ties into a crucial differential equation, known as the Laplace equation:
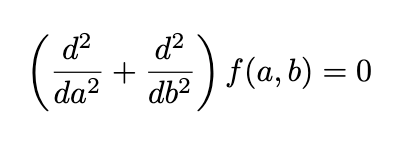
However, we can express this equation using our factorization method:
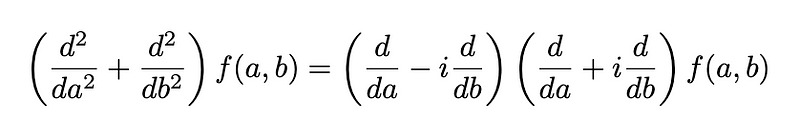
When we substitute any differentiable function of the form f(a+ib), it automatically satisfies Laplace’s equation.
The intriguing aspect of the solutions to these equations is their unique averaging or smoothing quality:
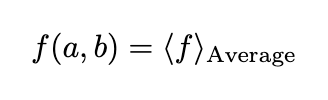
This averaging can be conducted using any circle of any radius surrounding the point (a, b). However, this property holds only if f(a, b) is well-defined throughout the circle (i.e., it has no singularities).
Technical Note: The proof of this averaging property is quite intricate, but we can glean insights from physics. The Laplace equation describes fluid flows or energy fields (i.e., potential flow or electric potential). To minimize total energy, the potential tends to smooth out, leading to the averaging property.
With this averaging characteristic, the proof of the fundamental theorem of algebra becomes straightforward. Consider our function 1/p(a+ib), relating it to an average:
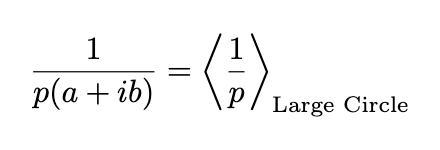
For any value of a+ib, we can identify an exceptionally large circle, sufficiently vast that 1/p becomes negligible, and the average around this large circle essentially yields zero! Hence, if 1/p has no singularity, it must indeed be 0, which is impossible. Therefore, a value must exist such that p(a+ib) = 0, creating a singularity that invalidates this averaging argument.
Epilogue
In conclusion, by conceptualizing a solution to the simple yet impossible equation x² + 1 = 0, we discover a profound link between algebra and geometry, ultimately demonstrating that all algebraic equations can now be solved.
This extends to the broader concept of analytic functions, allowing even more complex equations to have solutions. Below are a few examples (showing only one of many potential solutions):