Chapter 1: The Impact of Calculus

Since the groundbreaking work of Leibniz and Newton, calculus has dramatically influenced the scientific landscape across various fields such as physics, engineering, biology, and mathematics. It serves as a fundamental instrument in our quest for understanding and innovation.

Calculus can be approached from multiple angles. Practically, it relates to the concept of rates of change, which applies to physical laws expressed through differential equations. Conversely, from a mathematical standpoint, differentiation can be viewed as a transformation that shifts functions from one space to another. While I won’t delve deeply into the intricacies of function spaces, it's important to recognize that a collection of functions can exhibit characteristics similar to vector spaces with a foundational field, like the real numbers.

This transformation aligns with the operator d/dx, which possesses two significant properties:

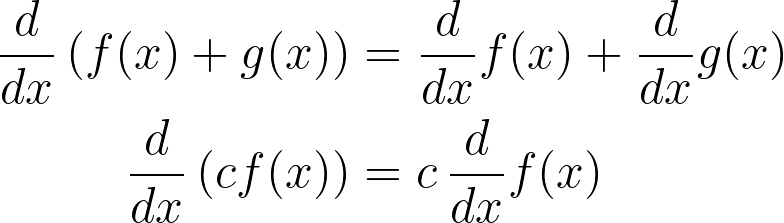
These properties together are termed linearity. For example, the real function f(x) = kx, where k is a real number, also upholds the conditions of linearity:

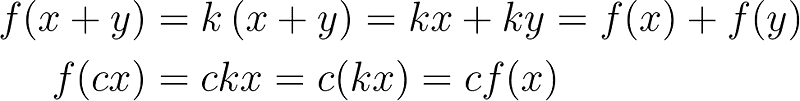
This concept parallels linear transformations studied in linear algebra, where matrices serve as examples of linear transformations among vector spaces, also satisfying linearity.

The first property of linearity is crucial, as it indicates that the structure of a function space is preserved with respect to addition. It acts as a translator between two realms, facilitating the transfer of additive structures. Such functions are known as homomorphisms.

In this article, we will introduce a different kind of operator—a transformation between function spaces that resembles logarithmic behavior rather than linear. We will derive several rules analogous to the previously defined differential operator, including the product and chain rules. Interestingly, our operator exhibits homomorphic behavior, transitioning from a multiplicative function space to an additive one.

The operator in question is called the logarithmic derivative, defined as follows:

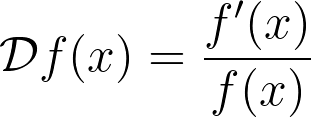
Before diving deeper, let's explore some of the appealing properties of this operator. A relevant question arises regarding its effect on constants. As demonstrated, we find:

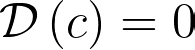
Crucially, it transforms products into sums and divisions into differences:

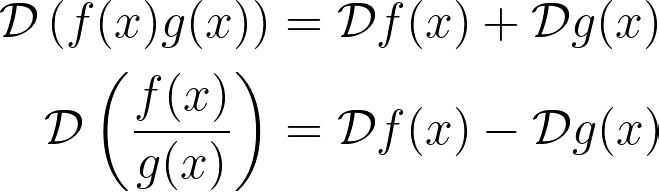
This result can be established using its definition and standard differentiation rules. Notably, when a constant multiplies a function, the constant disappears upon logarithmic differentiation:

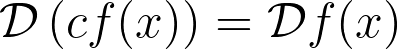
This property also allows for rearranging subtraction between function arguments in the operator, expressed as follows:

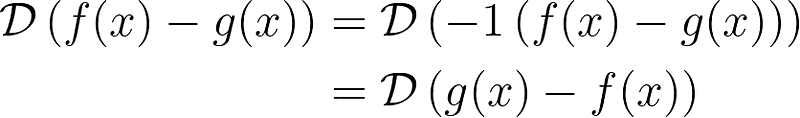
Next, let’s outline the chain rule applicable to this operator:

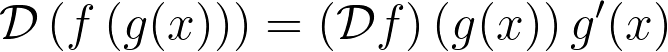
The derivation is straightforward:

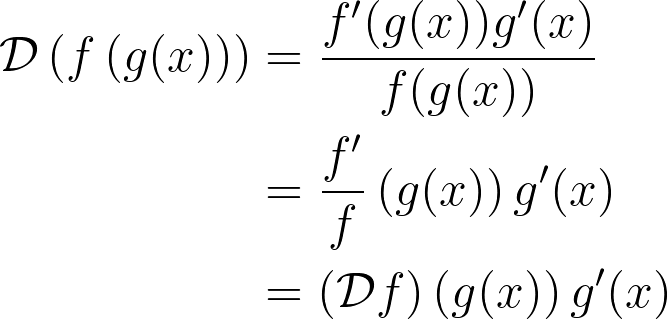
Its resemblance to the chain rule of the differential operator is quite remarkable. Additionally, we have the power rule:

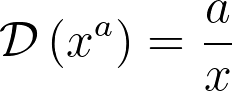
In particular, we derive two useful formulas:

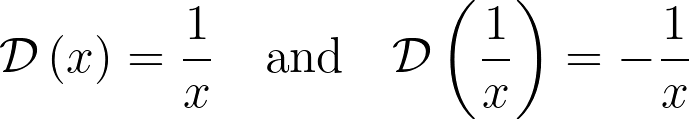
At this juncture, you may be curious about the eigenfunctions associated with this operator. For the standard differential operator, the eigenfunction is the scaled natural exponential function, which satisfies:

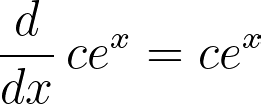
Conversely, for the logarithmic derivative, we find:

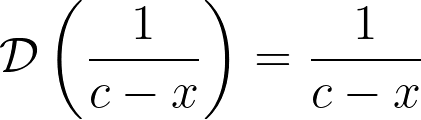
This holds for all constants c, positioning these functions as eigen elements within the defined function space.

Now that we have established several rules for the logarithmic derivative, let’s put them to use. We will begin by calculating the logarithmic derivative of the sine function. Utilizing the definition, we can quickly derive:

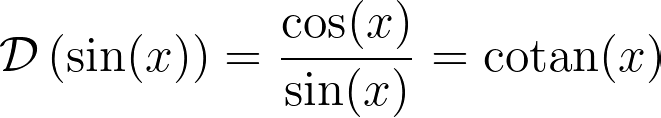
Recall that the sine function can be expressed as an infinite product:

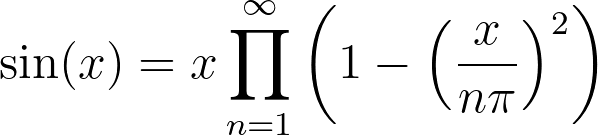
By applying the aforementioned rules, we can convert the infinite product into a series by taking the logarithmic derivative of both sides:

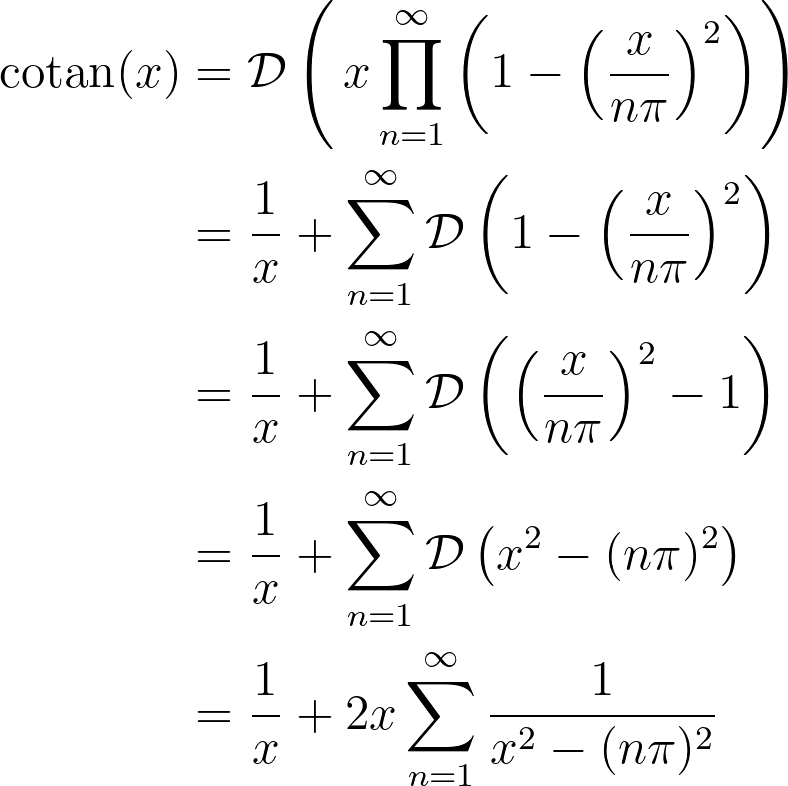
In this process, we utilized several established rules: the power rule, the product-to-sum rule, rearrangement of subtraction, the vanishing constant, and the chain rule.

To ensure that the product-to-sum rule holds for an infinite product, certain conditions must be met. These include:

1. The factors within the product must be holomorphic (i.e., analytic) over an open subset D of the complex plane.
2. None of the factors can be identically zero within D.
3. The product must converge locally uniformly to a function f.

When these criteria are satisfied, the resulting series obtained from the logarithmic derivative converges locally uniformly on the following set:

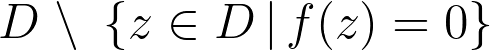
The backslash here indicates set-difference.

This discussion may seem technical, but what does it imply? A complex function is considered holomorphic if it is "complex differentiable," which entails a stronger requirement than real differentiation. In fact, if a complex function is differentiable at one point, it is differentiable at all points, thus making it analytic (i.e., it can be represented by a power series). This principle does not generally hold true for real functions.

Moreover, if a holomorphic function is zero on any open subset of a connected set D, it must be zero throughout D. This is not the case for real functions.

In essence, holomorphic functions exhibit global properties within any arbitrarily small subset of their domain.

The Identity Theorem mentioned above is vital, underpinning proofs related to the analytic continuation of certain functions. Locally uniform convergence is a technical stipulation that is less stringent than uniform convergence but more rigorous than pointwise convergence. If the product converges uniformly, it also converges locally uniformly.

Returning to the resulting series, it would be preferable to eliminate the ? in the denominator. A substitution and multiplication reveal this identity in a more recognizable form:

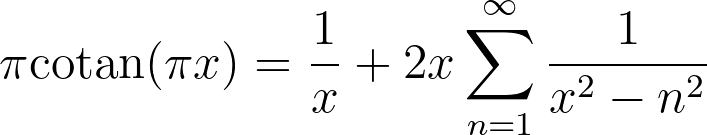
Leonhard Euler was the first to uncover this series, utilizing the infinite product representation of the sine function. You can discover more about Euler’s remarkable findings here.

The logarithmic derivative operator is widely employed in complex analysis and analytic number theory, serving as a crucial tool in the exploration of the Riemann Zeta Function. It is also utilized alongside contour integration to determine the zeros and poles of meromorphic functions within closed contours.

With our newfound understanding of this operator, why not explore further and discover additional series derived from infinite products?