Understanding the Diffie-Hellman Key Exchange: A Group Theory Approach
Written on
Chapter 1: Introduction to Cryptography
The primary objective of cryptography is to enable two parties to securely share a coded secret over a public channel. To maintain security, this secret must remain confidential, meaning unauthorized individuals should not be able to decipher it, even if they access the encrypted data. Most encryption techniques depend on a key, known only to the involved parties, which must be kept private. For the purpose of this discussion, we can represent this secret as a number, denoted as s. The techniques employed to securely communicate this key are referred to as key exchanges. A classical and straightforward method for achieving this is through the Diffie-Hellman protocol. This protocol leverages fundamental principles of group theory to safeguard secrets and is applicable across various mathematical groups.
Section 1.1: Cyclic Groups Explained
The initial step involves selecting a mathematical group that is cyclic. As previously outlined, a group is a mathematical entity comprising certain elements. For this scenario, we will consider a finite number of these elements, along with a binary operation that allows us to 'combine' two elements within the group. The following conditions are essential for something to be formally classified as a group:
- There exists a group identity, labeled e, such that for every element g in G, the equation e · g = g · e = g holds true. This signifies that the group must contain a unique 'do nothing' transformation.
- For every symmetry transformation in the group, there is a unique inverse corresponding to each element g in G, denoted as g'. This requires that g’ · g = g · g’ = e.
- The property of associativity indicates that the order of multiplication does not affect the result; for all g1, g2, g3 in G, it follows that g1 · (g2 · g3) = (g1 · g2) · g3.
Moreover, a cyclic group is one where every element can be represented as repeated additions of a single, unique element to itself until it reaches the identity. This concept can be likened to clock arithmetic, where the set of numbers modulo n under addition forms a cyclic group, and the unique element that generates the entire group is known as the generator.
The first video titled "Explaining the Diffie-Hellman Key Exchange" provides an accessible overview of the protocol, illustrating its significance in secure communications.
Section 1.2: The Diffie-Hellman Protocol
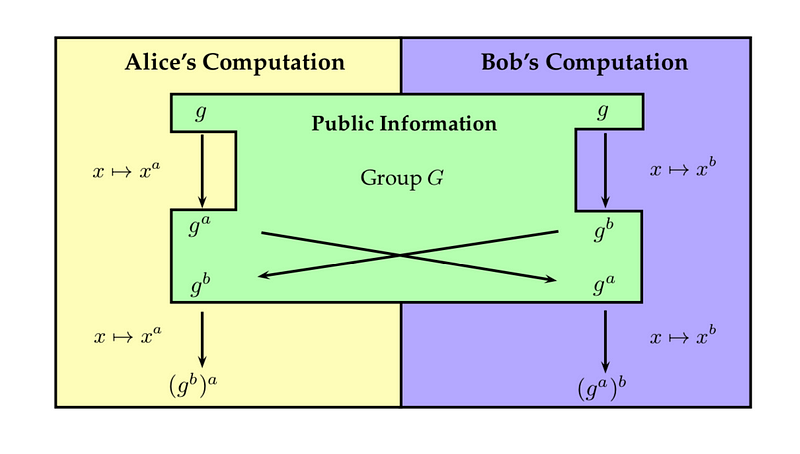
The Diffie-Hellman protocol aims to facilitate the sharing of a secret key between two parties without disclosing it to anyone else. Let’s consider two participants, Alice and Bob, each possessing a private key represented as a and b. They can select a publicly known group G, which is assumed to be cyclic and has a generator.
Suppose Alice wishes to share a generated secret key with Bob. In the initial step, she raises the generator to the power of a and transmits this value to Bob. Subsequently, Bob raises the received value to the power of b, resulting in g^(ab), which becomes the secret key. Afterward, he sends Alice g^b, and she performs a similar operation.
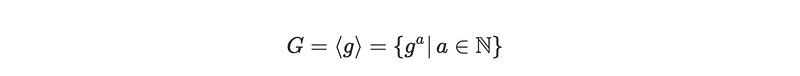
The cyclic group generated by a prime number consists of numbers modulo p, where multiplication serves as the group operation. The cyclic nature of this group is proven using Fermat’s Little Theorem, which confirms the existence of a unique generator. When G is such a group, it becomes challenging for an adversary to compute the values of a and, consequently, the secret key.
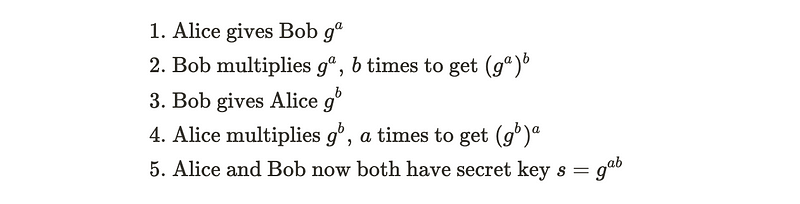
Chapter 2: Elliptic Curves and Their Applications
The second video, "Secret Key Exchange (Diffie-Hellman) - Computerphile," delves deeper into the Diffie-Hellman method, exploring its implementation and potential vulnerabilities.
Section 2.1: Utilizing Elliptic Curves
The Diffie-Hellman protocol is adaptable, allowing for the use of any cyclic group, including groups formed by points on an elliptic curve. It may not be immediately evident why points on an elliptic curve can constitute a group, but this section will clarify that. Start with a field F, which could be the real numbers, complex numbers, or the multiplicative group of integers modulo p. An elliptic curve consists of points in two dimensions that satisfy a specific equation.
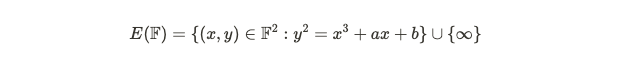
To add two points, A and B, on the elliptic curve, a line is drawn connecting them, which intersects the curve at a third point. This point is then reflected across the x-axis to yield A+B. For adding A to itself, the tangent line at point A is used to find where it intersects the curve, followed by a reflection across the x-axis.
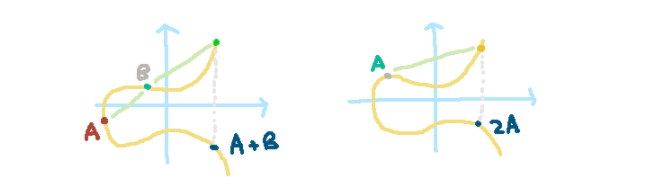
By viewing this as a cyclic group, we can apply the Diffie-Hellman procedure to securely exchange keys. Despite its robustness, the Diffie-Hellman protocol is susceptible to various attacks, including the Pollard Rho algorithm.
Section 2.2: Vulnerabilities and Future Directions
Recent advancements indicate that Diffie-Hellman could be compromised by quantum computers. In the subsequent post, I will explore how isogenies may provide a defense against potential quantum attacks.