Understanding Curvilinear Coordinates: A Comprehensive Guide
Written on
Chapter 1: Introduction to Curvilinear Coordinates
Coordinate systems play a crucial role in physics calculations. The complexity of a problem can drastically change depending on the coordinate system utilized. While Cartesian coordinates are straightforward and often sufficient, other systems, such as polar coordinates, can provide greater convenience in specific scenarios, particularly in areas like planetary motion. This article delves into the nature of curvilinear coordinates, their applications, and their connection to Cartesian coordinates.
Section 1.1: Polar Coordinates Explained
To illustrate curvilinear coordinates, let's examine polar coordinates and the transition from Cartesian to polar systems. The vector v exists independently of any coordinate system; it simply denotes a point in the plane. However, when we adopt a coordinate system, such as Cartesian coordinates, we define base vectors associated with that system, allowing us to express the vector v in terms of these base vectors.
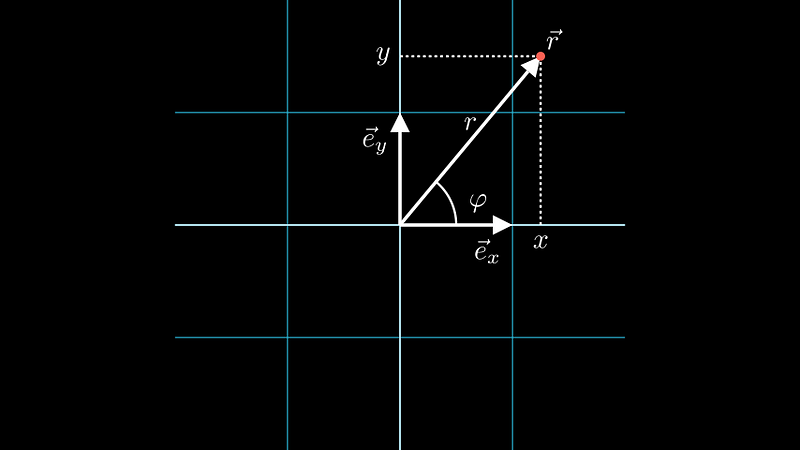
In Cartesian coordinates, the components of vector v can be expressed as its components along the corresponding base vectors.
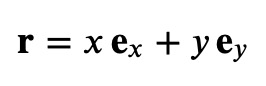
In contrast, we can also describe the vector using the angle θ and the distance r from the origin, which constitute the polar coordinates of the point. What about the base vectors er and eθ corresponding to (r, θ)? These are illustrated in the subsequent animated figure.
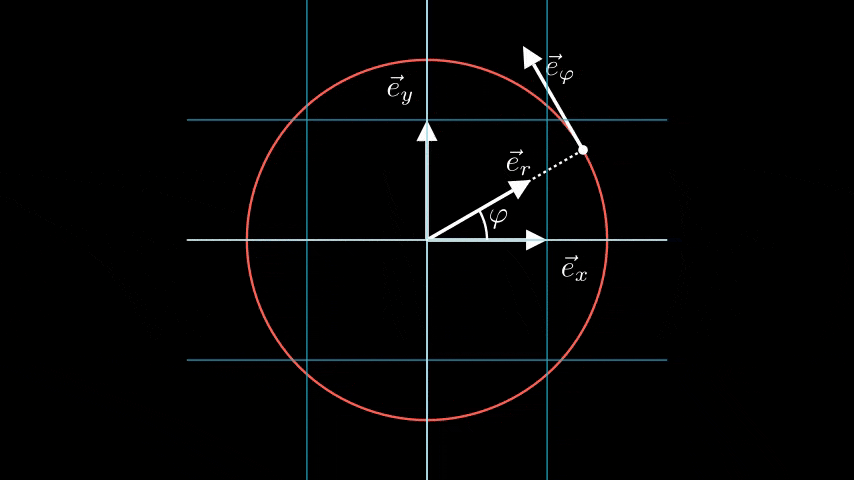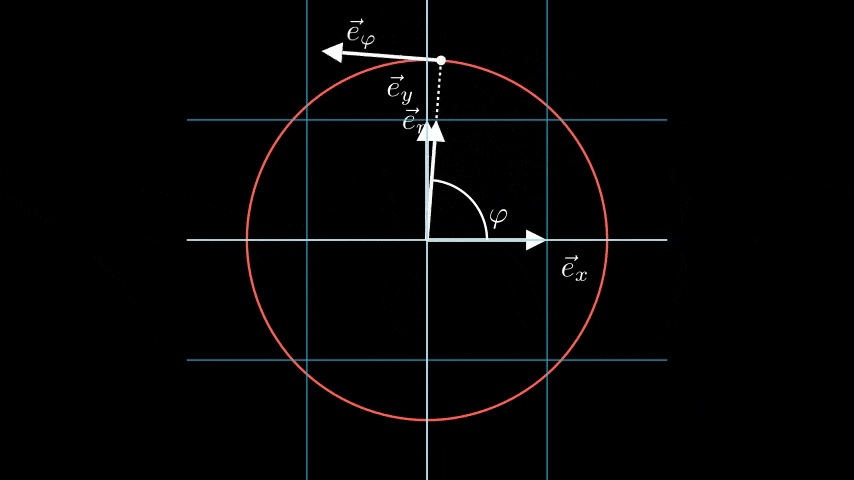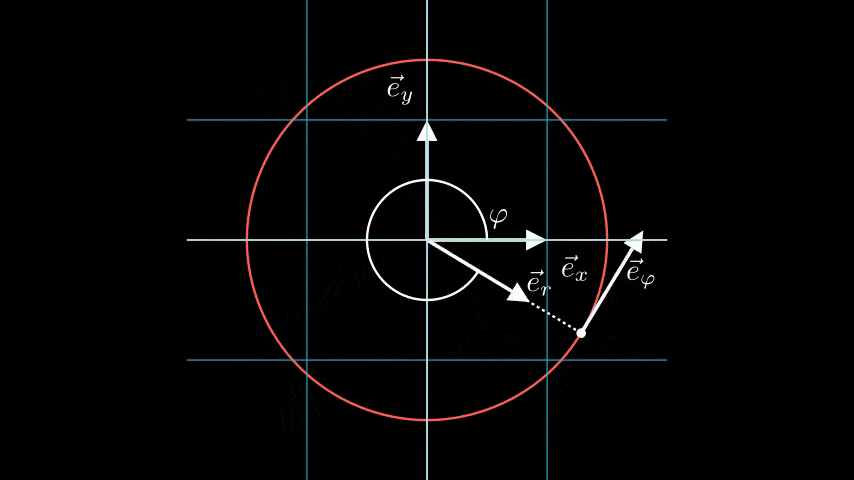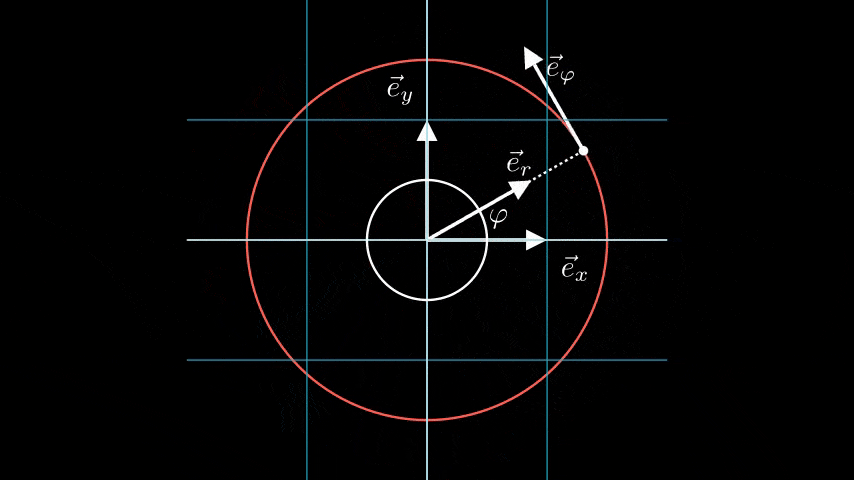
It’s important to note that, unlike the fixed base vectors i and j in Cartesian coordinates, the base vectors er and eθ vary at every point in the plane, which is a defining characteristic of curvilinear coordinates. The base vectors for polar coordinates can be expressed in Cartesian terms as follows:
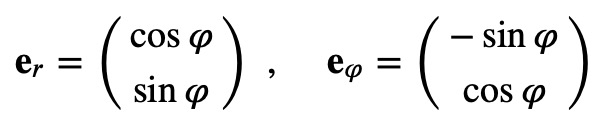
Calculating the scalar products of these vectors reveals that they are perpendicular to each other and of unit length, confirming they are indeed unit vectors.
Section 1.2: Deriving Base Vectors
How do we derive the base vectors from the coordinates? Given coordinates (r, θ), we can obtain the base vectors at the point represented by (r, θ) by holding one variable constant while varying the other. The path traced while varying θ while keeping r constant forms the θ-coordinate line, and the tangent to this line at (r, θ) gives us the base vector in the θ direction, eθ. The base vector in the r direction is derived similarly.
If all coordinate lines are straight, you have a Cartesian system. If at least one line is curved, you have curvilinear coordinates.
The relationship between Cartesian and polar coordinates can be expressed mathematically as follows:
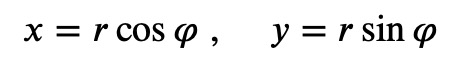
In general, for two coordinate systems in a d-dimensional space, we have d functions relating them. These functions must be invertible, except possibly on a lower-dimensional subspace. To determine the validity of a coordinate transformation, we examine the differentials and express them compactly as:
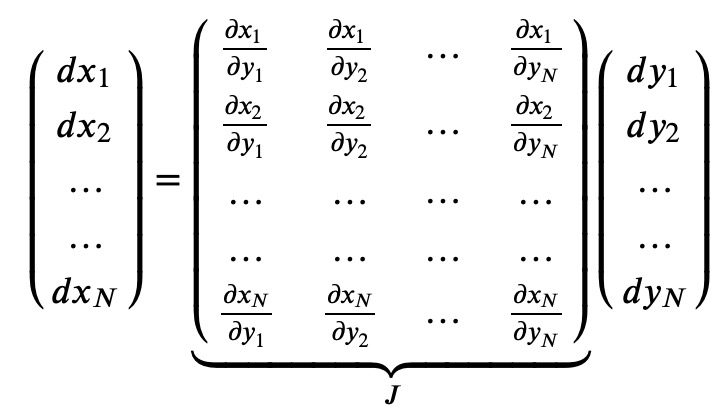
The matrix containing the partial derivatives is known as the Jacobian matrix J. The transformation is invertible if the Jacobian matrix is invertible; square matrices are invertible if their determinant is non-zero.
The Jacobian matrix for the transformation from Cartesian to polar coordinates is:
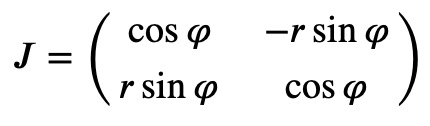
It has a determinant of det J = r, indicating that the transformation becomes non-invertible at the origin (r = 0, θ). This is acceptable since it represents a one-dimensional set.
Chapter 2: Velocity in Curvilinear Coordinates
In physics, coordinates and derivatives are fundamental concepts. For instance, if x(t) denotes the position of an object over time, its velocity is the time derivative of its position:
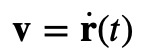
The vector v can be expressed as:
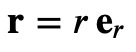
When applying the time derivative in curvilinear coordinates, we must consider that the base vectors also change with the body’s motion. This necessitates the use of the product rule:
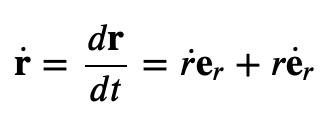
By utilizing the chain rule of differentiation, we arrive at:
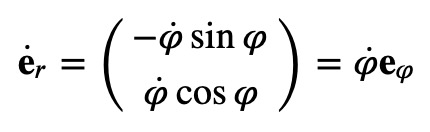
Thus, the velocity can have components both in the radial direction and in the θ direction. The use of unit vectors that are orthogonal is highly advantageous. Systems that possess these features are classified as complete orthonormal systems—where "complete" indicates that any point can be expressed in terms of these vectors, and "orthonormal" implies they are of unit length and mutually perpendicular.
In polar coordinates, the kinetic energy of a mass m can be expressed as follows:
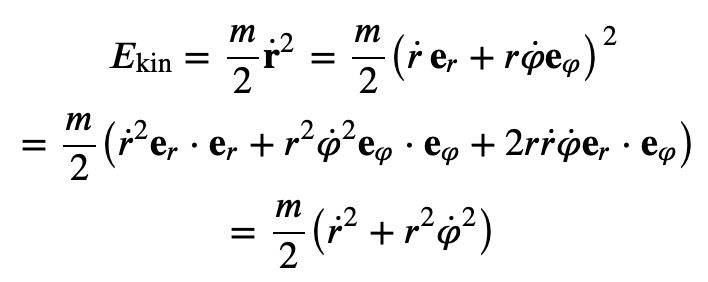
Many terms simplify to either factors of one or zero, illustrating the utility of this coordinate system. While this overview touches on the basics of curvilinear coordinates, there is much more to explore, including vector analysis identities like gradients and curls. This foundational understanding sets the stage for future discussions on topics such as general relativity.
The first video titled "Vector calculus in curvilinear coordinates! (a helpful intro)" provides an engaging introduction to the concept of vector calculus within curvilinear systems.
The second video, "Lecture14 - Part1: Curvilinear Coordinate Systems in 2D," offers a deeper exploration into curvilinear coordinate systems, particularly in two dimensions.