Understanding the Bouncing Ball Puzzle: A Guide to Limits
Written on
Chapter 1: Introduction to the Puzzle
Recently, while diving into literature on the concept of 'limits', I stumbled upon the bouncing ball puzzle, which I found quite engaging. I thought it might pique your interest as well.
The puzzle is straightforward: Imagine you possess an ideally elastic ball. You climb to the top of a 4-meter ladder and release this ball onto a hard floor below. The ball reaches a height of 3 meters on its first bounce, then on each subsequent bounce, it rebounds to three-quarters of the height of the previous bounce.
Assuming this ball can overcome all frictional forces, it will bounce infinitely. However, here’s the intriguing part: even after bouncing infinitely, it will eventually come to rest after a finite amount of time.
Your task is to calculate the total distance the ball has traveled in the air (both up and down) after all its bounces. Are you ready to take on this challenge?
If you find yourself stuck or unsure where to begin, you might want to check out my article on limits for some hints. But be cautious, as reading it might simplify this puzzle significantly.
Spoiler Alert: If you prefer to solve this puzzle independently, I recommend pausing here. The following sections will reveal the solution.
Section 1.1: Setting Up the Problem
The crux of this puzzle lies in the starting point. Once you determine where to begin, the rest becomes much more manageable. Recall the statement from the introduction:
“The ideally elastic ball comes to rest after a finite time despite bouncing infinitely.”
This situation hints at the concept of limits. Have you identified your starting point? If not, don't worry. We’re dealing with a series here. Let's temporarily disregard the initial drop of 4 meters. For the first bounce, the ball ascends 3 meters (which is three-quarters of 4 meters) and then descends the same distance. This totals 6 meters for the first bounce (up and down).
On the second bounce, the ball travels three-quarters of 6 meters (up and down). This pattern continues indefinitely. If we denote the total distance the ball covers (starting from the first bounce) as 'x', the series can be expressed as follows:
x = 6 + (3/4)*(6) + (3/4)*(3/4)*(6) + (3/4)³ * 6 + …
With this series established, we can now proceed to solve the puzzle!
Section 1.2: How to Solve the Puzzle
At first glance, the series may seem daunting. How can one sum an infinite series? Doesn't it lead to infinity? This is where a solid grasp of limits becomes essential.
This series is convergent, meaning it will converge to a specific limit. If you want a quick understanding of limits, think of it as the sum of the series as it approaches infinity.
Our goal is to find the sum. Interestingly, computing the limit for such series is quite straightforward. Each term in this series decreases by a constant ratio.
There’s an easy method to calculate the sum of this series, which is easier to show than to explain. Take a look at the following illustration:
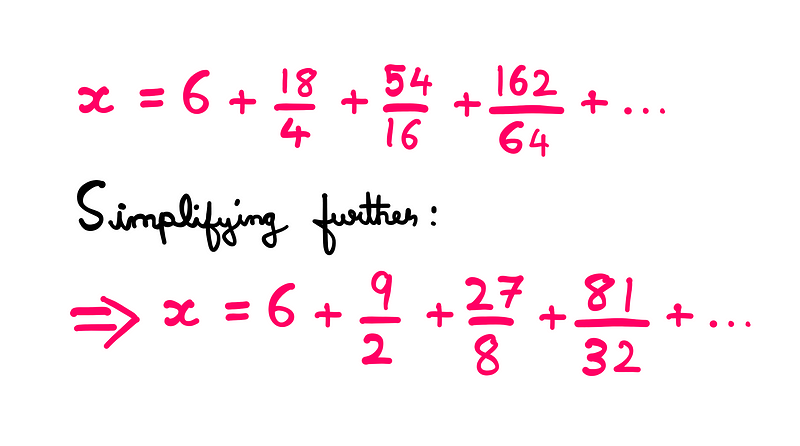
Knowing that each term is three-quarters of the preceding one, let’s multiply the entire series by its reciprocal (4/3):
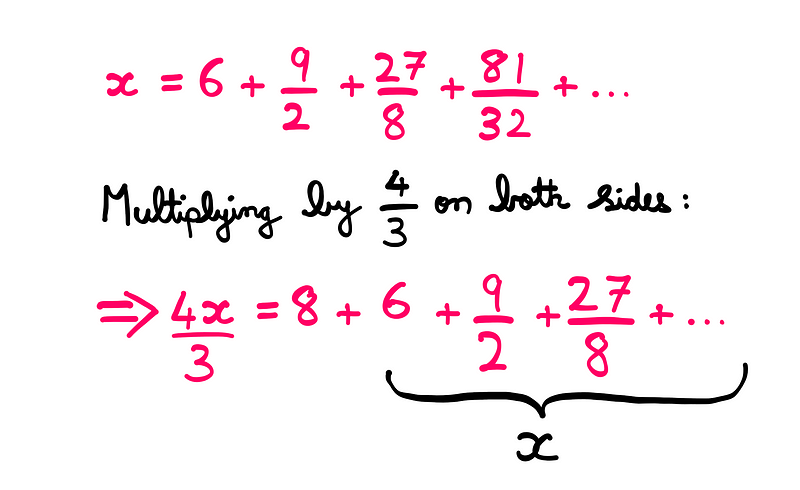
This manipulation leads us to a situation where the sum of all terms after the first term on the right equals the original series variable 'x'. From here, finding the solution becomes a straightforward algebraic task.
Chapter 2: Arriving at the Solution
We begin by substituting 'x' for the sum of all terms after the first term and simplifying the equation:
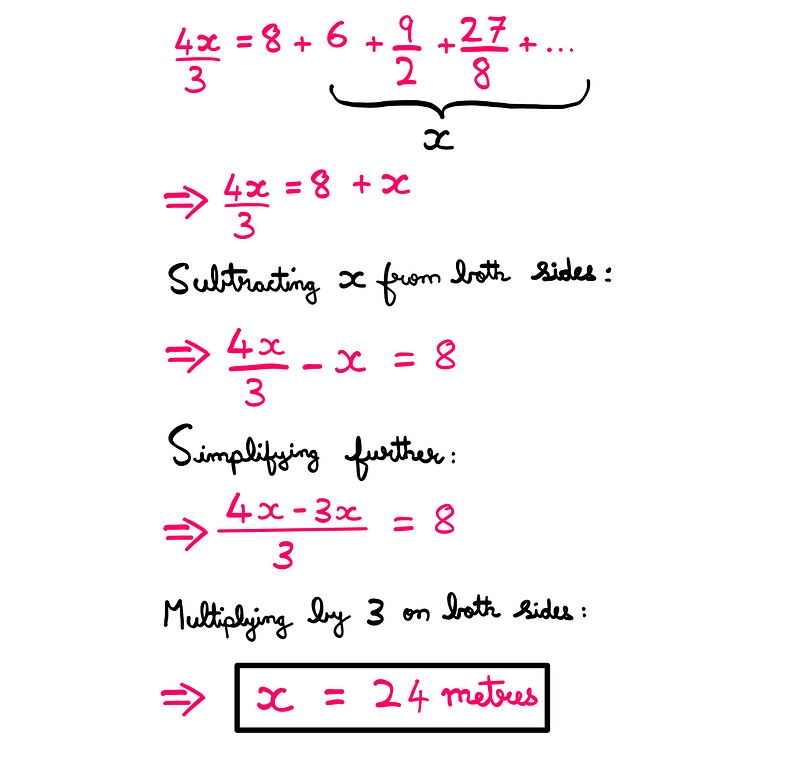
And there we have it! The limit or sum of the series at infinity is determined to be 24 meters. But before we celebrate, we must consider one last aspect: the initial drop height from the ladder.
Thus, the total distance the ball traveled in the air from the moment it was released is:
Total distance = x + 4 meters = 24 + 4 = 28 meters.
And that concludes our exploration of the puzzle!
To explore more of my work, check out the MAP available on my about page. Enjoy!
References and acknowledgments: Martin Gardner and Sam Loyd.
If you appreciate my content, consider supporting me on Patreon.
For further reading, you can access the original essay here.
Chapter 3: Additional Insights from YouTube
The first video titled "What If A BOUNCY BALL Had Puzzles? - Animal Well" explores fascinating scenarios with bouncing balls, providing context that enhances understanding of the puzzle.
The second video, "6-Piece Put Together Ball Puzzle - Fast and Easy," demonstrates a quick and straightforward approach to assembling ball puzzles, offering practical insights that complement our discussion.