Mastering Two Essential Integration Techniques in Mathematics
Written on
Chapter 1: Introduction to Integration Techniques
If you have delved into mathematics for any length of time, you likely recognize the immense value of integration and its applications across various mathematical fields. Mastering integration often hinges on familiarity with specific techniques or prior experience with similar problems. Essentially, to enhance your integration abilities, practice is essential! Experience plays a crucial role when tackling integrals.
In this discussion, we will introduce two significant integration methods and work through two examples that utilize these techniques. We will first explore each technique to understand its fundamentals.
Section 1.1: Feynman’s Technique
Feynman’s technique, also known as differentiating under the integral sign, involves defining an integral I(λ) in terms of a variable λ and differentiating it with respect to λ. This process often simplifies the integral into a more manageable form. This technique is also recognized as the Leibniz integral rule. Let’s clarify this rule:
We can only apply this rule if the function f(x, λ) is continuous and continuously differentiable. Let’s illustrate this with a practical example.
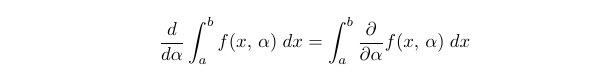
How might you consider using Feynman’s technique for the given integral? A common hint is encountering a variable raised to a power alongside a natural logarithm. This often suggests Feynman’s approach. We start by defining I(λ) and calculating its derivative.
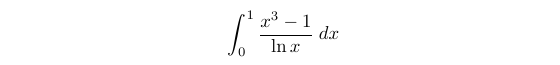
Notice how differentiating with respect to λ allows us to eliminate the ln x in the denominator, resulting in a more approachable integrand. We can now proceed to compute this integral.
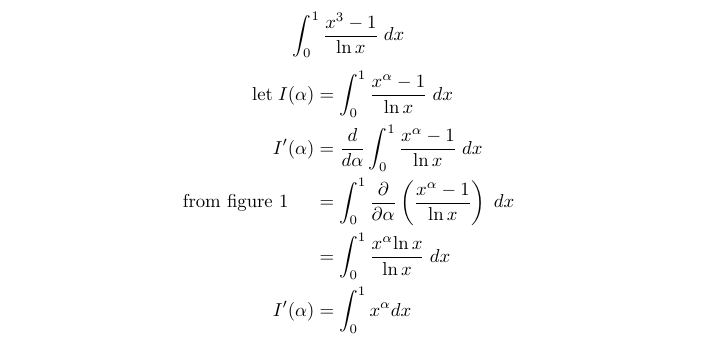
Next, we integrate both sides with respect to λ, ensuring we account for the constant of integration.
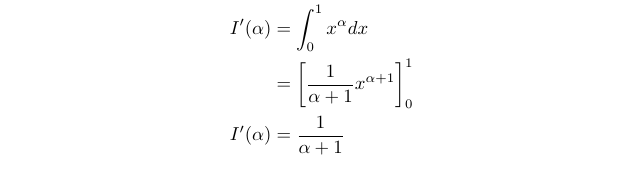
Now we have an expression for I(λ), but we need to eliminate the constant of integration. To do this, we substitute a value for λ, yielding a straightforward solution for I(λ). In this instance, we can select λ=0.
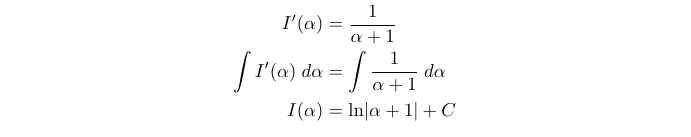
Finally, we substitute λ with the desired value of 3 to determine our original integral.
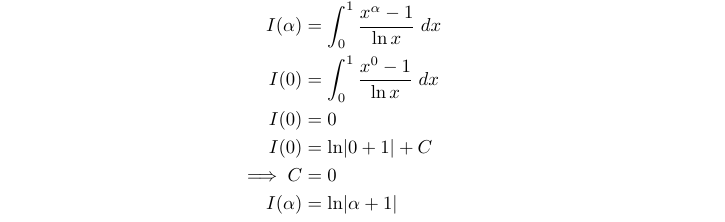
We hope you now appreciate the usefulness of this technique. Let’s transition to discussing Weierstrass substitution.
Section 1.2: Weierstrass Substitution
The Weierstrass substitution is particularly effective for integrals involving trigonometric functions. The core idea of this technique is to let t=tan(θ/2), allowing us to express sin(θ) and cos(θ) in terms of t, which frequently leads to an integrable form. To illustrate this technique, let’s examine the following integral:
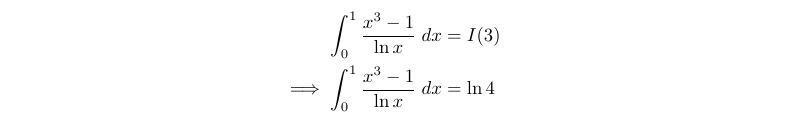
We will now make the substitution t=tan(θ/2) and work through the solution.
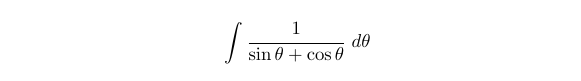
If you’re familiar with the derivatives of inverse hyperbolic functions, you may have reached the solution earlier in terms of artanh.
Now that we understand both techniques, let's solve one more integral that incorporates both methods!
Chapter 2: Applying the Techniques
The first video titled "The Single Most Overpowered Integration Technique in Existence" provides an overview of powerful integration methods that can greatly enhance your understanding.
The second video, "One of the Most Powerful Integration Techniques You Should Know," delves deeper into integration strategies that every mathematics enthusiast should grasp.
Let’s consider the following problem:
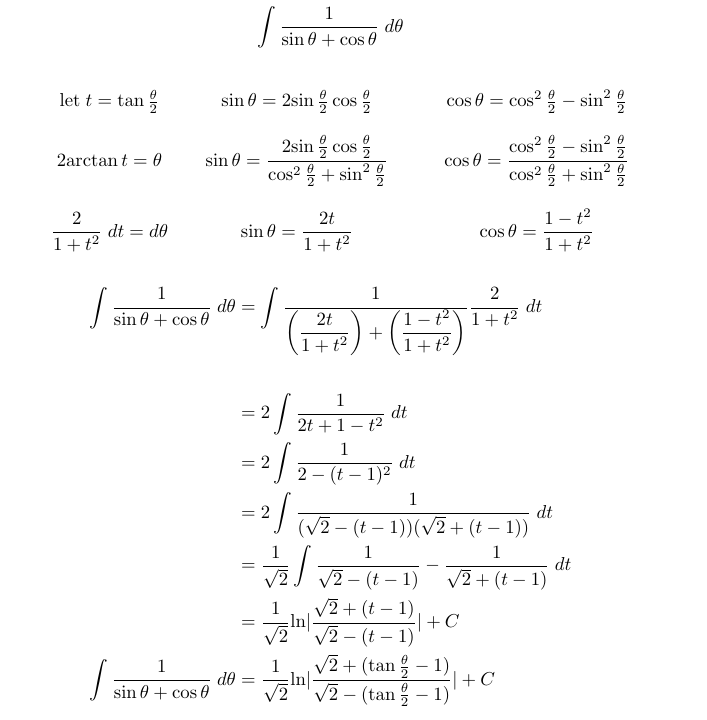
Before reviewing the solution, take a moment to think about which technique would be best to apply first.
Section 2.1: The Solution
We will initiate the process with the Weierstrass substitution. What prompts this choice? Whenever trigonometric functions are present, using this substitution often leads to a more manageable integrand. Additionally, there are no clear indications of applying Feynman’s technique at this point. Thus, let’s begin.
Before applying the Weierstrass substitution, we may wish to simplify the integrand by substituting 2x=θ.
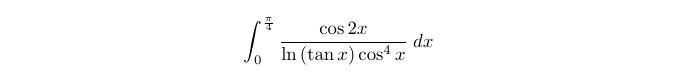
Observant readers might notice that the final integral mirrors the one we analyzed with Feynman’s technique, albeit multiplied by -1, allowing us to apply Feynman’s technique effectively and derive:

And that concludes our exploration of these techniques. We hope you now have a clearer understanding of both methods and their potential applications. Thank you for reading, and feel free to share your thoughts on these techniques!