Chapter 1: Introduction

In this article, we will delve into the concepts of basis functions and regularization, demonstrating their application through theoretical explanations and Python implementations.

As we explore this topic, we will utilize a series of posts that provide deeper insights. For more detailed information, you can visit my personal blog.

Chapter 2: Basis Functions

In the previous discussion, we examined the linear regression model.

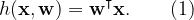
A model is considered linear if it is linear concerning its parameters, rather than the input variables. This characteristic limits its ability to accommodate nonlinear relationships. To address this, we can enhance the model by substituting the input variables with nonlinear basis functions derived from these inputs.

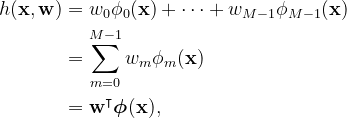
By employing nonlinear basis functions, we enable our model to adapt to the nonlinear relationships present in the data, leading to what we refer to as linear basis function models.

Previously, we explored an instance of basis functions where we augmented a simple linear regression model using powers of x:

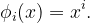
Another frequently used basis function is the Gaussian function.

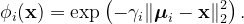
Following a similar derivation from our previous analysis, we determine the maximum likelihood estimates for the weights and biases as follows:

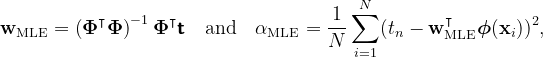
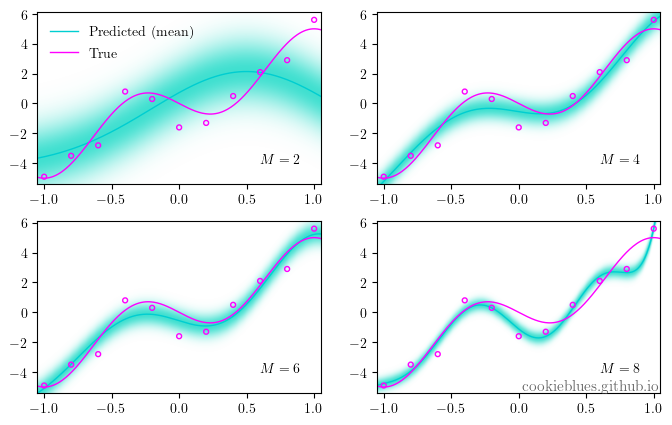
The image below depicts a linear basis function model utilizing M-1 Gaussian basis functions. As we increase the count of basis functions, the model improves until we reach a point of overfitting.

Chapter 3: Implementation

Using the same dataset from previous discussions, we can implement the model described.

Chapter 4: Regularization

We touched on regularization in the previous post regarding Bayesian inference, describing it as a method to mitigate overfitting. By revisiting the objective function established earlier (with the addition of basis functions), we can integrate a regularization term.

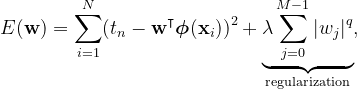
In this context, q > 0 signifies the type of regularization, and ? represents the degree of regularization. The most prevalent values for q are 1 and 2, known as L1 and L2 regularization, respectively. When applying L1 regularization, we refer to it as lasso regression; with L2 regularization, it becomes ridge regression.

The objective function for ridge regression is particularly useful as it is a quadratic function of w, resulting in a unique global minimum. The solution is given by:

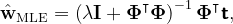
The regularization term does not affect ?, allowing it to remain unchanged from its value without regularization. As we introduce regularization, the focus of model selection shifts from determining the optimal number of basis functions to identifying the best value for the regularization parameter ?.

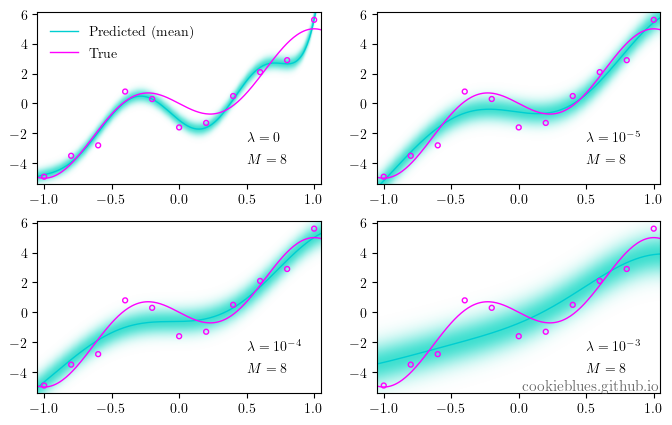
The subsequent illustration shows a linear basis function model with different values of ?, while maintaining a constant number of basis functions (M=8). We can observe that even though we start with overfitting, adjusting the regularization parameter ? effectively mitigates it. Interestingly, excessive regularization can lead to underfitting, resulting in increased uncertainty.

Chapter 5: Conclusion

In conclusion, a model's linearity pertains to its parameters, not the inputs. By augmenting linear regression with basis functions, we create linear basis function models, such as polynomial regression. Regularization serves as a vital technique to curb overfitting, with various types available, including L1 and L2 regularization.