The Challenge

You are the marketing director for a prominent news outlet planning to host a lottery for its 4 million subscribers. Each winner will receive a $1 million prize, with no additional prizes offered. Your boss has warned that the lottery will be deemed a marketing failure if no one wins and a commercial failure if more than two subscribers win. In either scenario, you will face significant repercussions, potentially losing your job. Tough situation!

Prove that, regardless of how the lottery is structured, your chances of retaining your job are less than 60%.

Analyzing the Approach

The design of the lottery will yield a specific probability, denoted as p, for any individual subscriber to win. Each subscriber either wins (with probability p) or does not win (with probability 1-p). Thus, the number of winners k follows a binomial distribution B(k, n, p), where n = 4,000,000.

We need to calculate the probabilities for the cases where k = 1 or k = 2.

Using Poisson Distribution for Approximation

Instead of directly applying the Binomial Distribution formula (which I’ll outline in an appendix as an alternative method), recall that for large n, the Poisson distribution serves as a good approximation for the Binomial distribution:

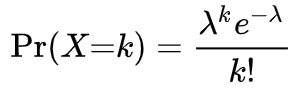
Here, k represents the number of winners, and λ = np. Focusing on the cases of k = 1 or k = 2, we can express the probability of having 1 or 2 winners as follows:

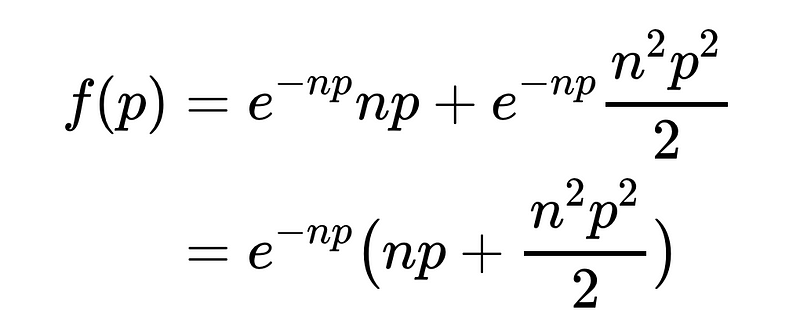
To maximize our chances of keeping our job, we differentiate this function and set it to zero to find the optimal p that maximizes f(p).

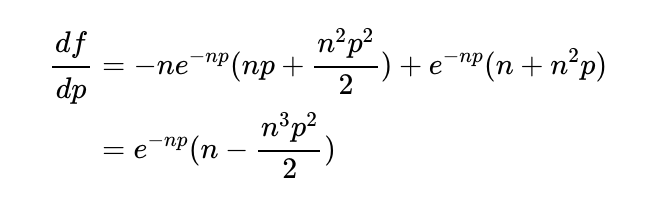
Solving the equation df/dp = 0 reveals that the first factor can never equal zero, indicating that the second factor must be zero. Thus,

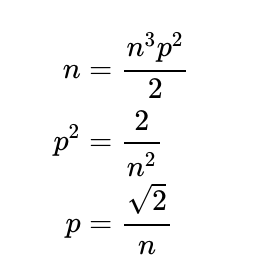
This means the maximum probability of having either 1 or 2 winners occurs when p = √2/n. Substituting this value into our function provides us with the maximum likelihood of job retention:

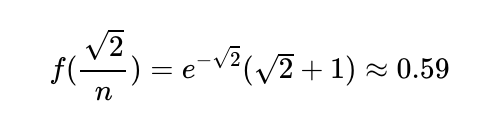
And with that, we have arrived at our solution!

Appendix: Alternative Method Using Binomial Distribution

We streamlined our calculations by utilizing the Poisson approximation, but if you are unfamiliar with it, the problem can still be solved using the Binomial formula, albeit with more algebraic steps.

Calculating the probabilities for 1 or 2 winners gives us:

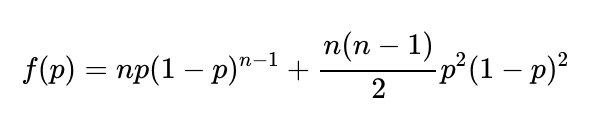
Differentiating this with respect to p and simplifying leads us to:

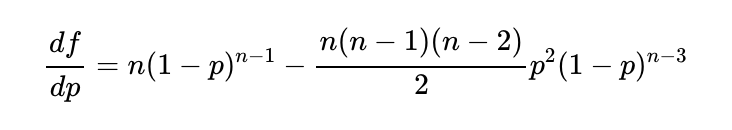
Setting this equal to zero allows us to find the maximum for f(p):

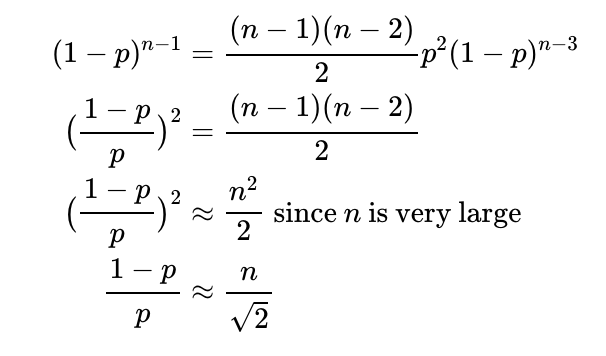
Rearranging gives us:

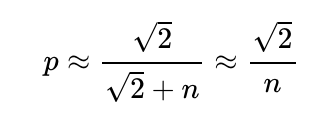
This leads us back to the same maximum value for p as in our previous Poisson approximation. Substituting this into our Binomial representation of f(p) yields:

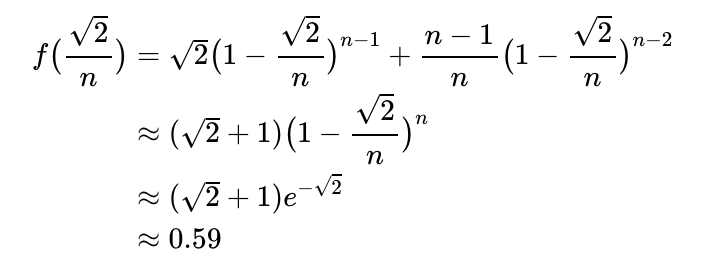
Which approach do you find more intuitive? I invite you to share your thoughts in the comments below.